素因数分解(1)　Pollardのρ法

RSA暗号が素因数分解の難しさを安全性の根拠にしていることからわかる通り、大きな数の素因数分解は非常に難しいです。
今のところ、200桁程度の数の素因数分解が限界のようです。

素因数分解(1) Pollardのρ法 - wacchoz’s note（今ここ）
素因数分解(2) p-1法、p+1法、楕円曲線法 - wacchoz’s note
素因数分解(3) フェルマー法、２次ふるい法 - wacchoz’s note

素因数分解アルゴリズムはいくつかの方法が知られています。
ざっくり分けると

p-1法、p+1法、楕円曲線法
フェルマー法、２次ふるい法、数体ふるい法

の2つのカテゴリーになりますが、今回紹介するPollardのρ法は、どちらにも属しません。

Pollardのρ法は、1975年にポラードが考案した方法です。古典的な方法で、ある程度小さい素因子をもつ場合にしか適用できないものの、他のアルゴリズムとは一風変わった面白い手法です。
ポラード・ロー素因数分解法 - Wikipedia

まず素数 $p$ を適当に１つとり、
$a_1 = 2 \\ a_{i+1}=a_i^2+1 \quad\text{mod }p\quad(i=1,2,\cdots)$

と数列を定義すると、 $a_i$ は疑似乱数のように振る舞います。
$a_{i+1}=a_i^2+1$ の数式自体にあまり意味はなく、他の数式でも疑似乱数のように振る舞うものであれば、何でもOKです。

$a_i$ は $0$ から $p-1$ の値をとるため、いつか同じ値をとり、その後、周期的に変化することになります。

例として、 $p=131$ としてみると、

$2, 5, 26, 22, 92, 81, 12, 14, 66, 34, 109, 92,\cdots$

となり、12項目と5項目が一致しました。この後は周期7で繰り返すことになります。

100000までの素数で、何項目で初めて一致する値が出現するかをプロットしてみます。
f:id:wacchoz:20190104233620p:plain

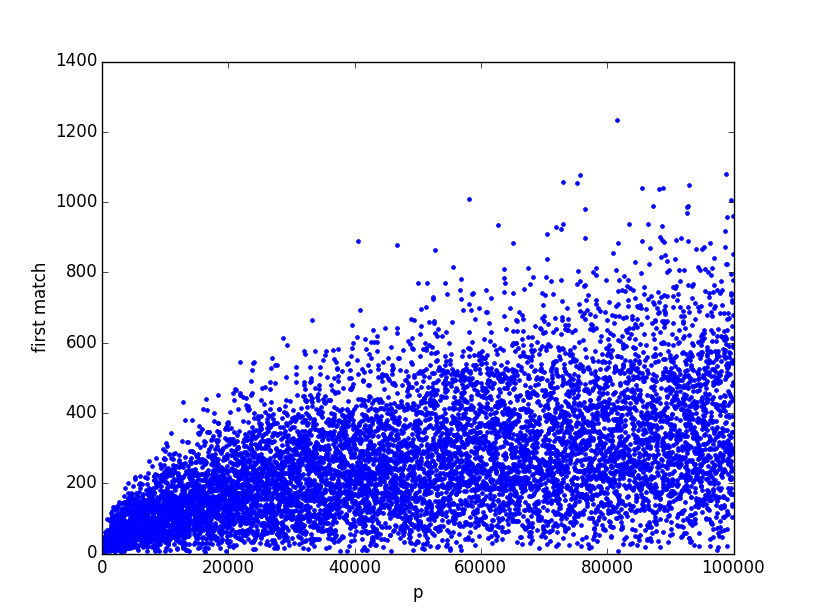
プロットしてみると、 $a_i$ は $0$ から $p-1$ の値をとりうるにもかかわらず、かなり早めに一致する値が出現することがわかります。
pが10^5ぐらいでも、数100項目で一致する値が出現します。

これに似た話は誕生日のパラドックスとしてよく知られています。
ランダムに23人を集めてきたら、その中に同じ誕生日の組がいる確率は50%を超え、70人いれば99.9%にも達します。

一般的には、 $n$ 通りの値をとる乱数があるとき、 $a$ 個の中に同じ値が出現する確率が50%を超えるのは、
$\displaystyle a\sim 1.1774\sqrt{n}$
で、 $n$ の値に比較して、かなり少ない個数で一致します。

さて、今までは素数 $p$ を法とした計算としていたが、素因数分解したい数 $N$ を法とした計算をしてみます。

$N=131\cdot 193=25283$ として、 $a_i$ を計算してみます。

$\displaystyle \begin{align} \text{mod }131& &\text{mod }25283 \\ 2 & & 2 \\ 5 & & 5 \\ 26 & & 26 \\ 22 & & 677 \\ \star 92 & & 3236 \\ 81 & &4535 \\ 12 & & 11147 \\ 14 & & 14948 \\ 66 & & 16834 \\ 34 & & 11693 \\ 109 & & 21069 \\ \star 92 & & 9131 \end{align}$
mod 25283の数列について、mod 131で考えると左側の数列と一致するので、9131と3236はmod 131で合同になるはずです。
実際、9131-3236は131で割りきれますし、 $N$ も131で割り切れるため、

$\text{gcd}(25283, 9131-3236) = 131$

となっています。そこで、

「合成数 $N$ が与えられたとき、 $a_k$ を計算時に、 $a_k-a_1, a_k-a_2, \cdots, a_k-a_{k-1}$ と $N$ との最大公約数を計算し、1でなければ終了。1であれば次のkに進む」

という方法が思いつきます。この方法は素因数を $p$ とすると、 $k=\sqrt{p}$ のオーダーまでにかなりの確率で素因子が見つかりますが、計算量が $k(k-1)/2$ に比例するため、結局のところ、 $p$ に比例する計算量となり、試し割り算と変わりません。

もっと効率的に計算するために、フロイドの循環検出法という手法を用います。
フロイドの循環検出法 - Wikipedia

ある $a_i$ から先は $a_i\equiv a_{i+K} \quad(\text{mod } p)$ となったとします。つまり数列のある箇所から先が周期 $K$ になったということです。
このとき、 $i\le K\cdot t$ になるように $t$ を大きくとると
$a_{Kt} \equiv a_{Kt+K} \equiv \cdots \equiv a_{Kt+Kt}$
となるため、 $m=K\cdot t$ とおくと
$a_{2m} \equiv a_m\quad(\text{mod } p)$
が成り立ちます。

ちなみに下図がρ法の名前の由来。
f:id:wacchoz:20190105225443p:plain:w240

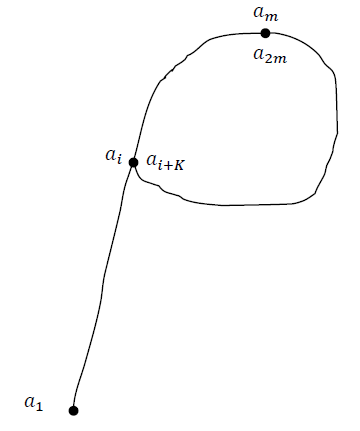
よって $1\lt \text{gcd}(a_{2m}-a_m, N) \lt N$ となる可能性が高く、そうなれば素因子が見つかったことになります。
$m$ の値はわからないため、小さい順に $a_{2k}-a_k$ を計算し、 $N$ との最大公約数をとります。

具体的には、2系統の数列 $(a_1, a_2, \cdots, a_k, \cdots)$ と $(a_2, a_4, \cdots, a_{2k}, \cdots)$ を生成し、順に $\text{gcd}(a_{2k}-a_k, N)$ を計算すればよいです。

計算量は平均的には $\sqrt{p}$ に比例となるため、 $O(N^{1/4})$ でおさえられます。

def gcd(a, b):
    if a<b:
        return gcd(b,a)
    r = b
    while a%b!=0:
        r = a%b
        a,b = b, r
    return r

def f(x):
    return x*x+1

N = 2**(2**6)+1 
print(N)
x=2
y=2
for i in range(10**7):
    x = f(x) % N
    y = f(f(y)) % N
    g = gcd(x-y, N)
    if 1<g<N:
        print(g)
        break
else:
    print("Fail")

参考文献

和田秀男, コンピュータと素因子分解, 遊星社, 1987
木田祐司, 牧野潔夫, UBASICによるコンピュータ整数論, 日本評論社, 1994