2019-05-27

素因数分解(3) フェルマー法、２次ふるい法

数学

以前の記事でもちらっと書きましたが、素因数分解のアルゴリズムは大きなカテゴリーが２つあり、そのうちの１つにフェルマー法、２次ふるい法、連分数法、数体ふるい法が属しています。
今回はフェルマー法、２次ふるい法を紹介していきます。

素因数分解(1) Pollardのρ法 - wacchoz’s note
素因数分解(2) p-1法、p+1法、楕円曲線法 - wacchoz’s note
素因数分解(3) フェルマー法、２次ふるい法 - wacchoz’s note（今ここ）

フェルマー法
２次ふるい法
- 平方数の構成法
  - 平方数の構成のプログラム例
- 「ふるい」とは？
参考文献

フェルマー法

素因数分解したい数 $N$ が $N=x^2-y^2$ と分解できたとします。そうすれば $N=(x+y)(x-y)$ と分解でき素因数分解できます。そこでこのような $x, y$ を探すことにします。
xの初期値として、 $x=\lfloor \sqrt{N} \rfloor + 1$ とします。
yの初期値は $y=\lfloor \sqrt{x^2-N} \rfloor$ とします。

$w=x^2-N-y^2$ を計算する
$w=0$ なら $x+y, x-y$ が素因数である
$w>0$ なら $y\leftarrow y+1$ とする
$w<0$ なら $x\leftarrow x+1$ とする
1.に戻る

$y$ の初期値が小さい値からインクリメントしていることかわかる通り、 $N$ の2個の素因子の値が近い場合に見つかるのが早いです。

２次ふるい法

２次ふるい法では
$\displaystyle x^2\equiv y^2 \pmod{N}$
となる $x, y$ を見つけることを目標とします。これが見つかれば
$\displaystyle x^2-y^2=(x+y)(x-y)$
が $N=pq$ の倍数になるということなので、うまくいけば $p, q$ が $x+y, x-y$ に分かれるかもしれません。そうなれば $\text{gcd}(x+y, N)$ が素因数として見つかることになります。

今、 $x$ を動かして $x^2$ を $N$ で割った余り $r$ をたくさん考えます。
$x^2 \equiv r \pmod{N}$
です。ここで、いくつかの $r$ をうまく組合せて平方数を作れれば、目的が達成されます。
これは各 $r$ を素因数分解して、各素数の指数を組み合わせて偶数を作ることを意味し、行列にGauss消去法を適用することにより計算できます。

もう少し具体的にすると、 $x=x_1, x_2, \cdots, x_t$ のときの $r_i=x_i{}^2-N$ となったとし、それぞれの $r_i$ を素因数分解すると
$\displaystyle r_i = p_1^{e_{i1}} p_2^{e_{i2}}\cdots p_m^{e_{im}}$ となったとします。
ここで指数を $\text{mod }2$ でベクトルとして並べて
$\displaystyle v_i=(e_{i1}\text{ mod }2, e_{i2}\text{ mod }2, \cdots, e_{im}\text{ mod }2)$
を作ります。
そして $v_1, v_2, \cdots v_m$ を行とする行列を作り、Gauss消去法で0だけの要素からなる行を作ります。Gauss消去法でどのような操作を行ったかがわかるように単位行列も用意し、単位行列にも同じ操作をしていきます。これでどの行を組み合わせることで0だけの要素からなる行ができるかが決定できます。

それらの行に対応する $r_i$ を掛け合わせれば平方数になるので、それを $y^2$ とすると、目標としていた $x^2\equiv y^2 \text{ mod }N$ が得られる。大抵の場合、 $\text{gcd}(x+y, N)$ で素因子が得られます。

平方数の構成法

具体例として $2,3,4,5,6,7,8,9,10,11$ からいくつかを選びだして、積が平方数になるものを探します。
これらの数の素因子は $2,3,5,7,11$ であるので、各値をそれらで素因数分解したときの指数の $\text{mod }2$ をベクトルとして並べ、右側に単位行列を並べます。

$\displaystyle \left( \begin{array}{ccccc|cccccccccc} 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{array} \right)$

この左半分をGauss消去すると以下のようになります。

$\displaystyle \left( \begin{array}{ccccc|cccccccccc} 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{array} \right)$

$3,5,7,8,9$ 行の左半分が $0$ になっており、平方数になったことを示しています。右半分を見るとどのような組合せなのかわかります。
例えば $5$ 行目は $1,2,5$ 列目が1になっているため、 $1,2,5$ 番目の数、 $2,3,6$ を掛け合わせると平方数になるとわかります。

平方数の構成のプログラム例

# -*- coding: utf-8 -*-

from pprint import pprint
from math import sqrt

# 「nをplistの素数で素因数分解したときの、各素数のべき乗の偶奇」を並べたベクトルを返す
# 素因数分解できなければNoneを返す
def factoring_vector(n, plist):
    ans = []
    for p in plist:
        e=0
        while n%p==0:
            n //= p
            e += 1
        ans.append(e%2)
    if n!=1:
        return None
    return ans

# Gauss消去
def gaussian_elimination(mat, row, col):
    
    for j in range(col):
        for i in range(j,row):
            if mat[i][j] == 1:
                pivot_row = i
                break
        else:
            continue
    
        if pivot_row != j:
            mat[pivot_row],mat[j] = mat[j],mat[pivot_row]
            pivot_row = j
        
        for i in range(pivot_row+1, row):
            if mat[i][j]==1:
                mat[i] = [(mat[i][k] + mat[j][k])%2 for k in range(len(plist)+len(rlist))]
    

if __name__ == '__main__':

    plist = [2,3,5,7,11]
    rlist = [2,3,4,5,6,7,8,9,10,11]
    mat = []
    
    # 行列を生成する    
    for k,r in enumerate(rlist):
        vec = factoring_vector(r, plist)
        # 単位行列のk行目
        identity = [ (1 if i == k else 0) for i in range(len(rlist)) ]
        
        print(r,vec)
    
        if vec is None:
            continue
        
        mat.append(vec + identity)
    
    pprint(mat) 
    
    # Gauss消去
    row = len(mat)
    col = len(plist)
    gaussian_elimination(mat, row, col)
            
    pprint(mat)
    
    # 行列の左半分が0になっている行を探す
    for i in range(row):
        allzero = True
        for j in range(col):
            if mat[i][j] == 1:
                allzero = False
                break
        if(allzero):
            n=1
            for j in range(len(rlist)):
                if mat[i][col+j] == 1:
                    n *= rlist[j]
            if n!=1:
                print(n,"は",sqrt(n),"の2乗")

2 [1, 0, 0, 0, 0]
3 [0, 1, 0, 0, 0]
4 [0, 0, 0, 0, 0]
5 [0, 0, 1, 0, 0]
6 [1, 1, 0, 0, 0]
7 [0, 0, 0, 1, 0]
8 [1, 0, 0, 0, 0]
9 [0, 0, 0, 0, 0]
10 [1, 0, 1, 0, 0]
11 [0, 0, 0, 0, 1]
[[1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0],
 [0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0],
 [0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0],
 [1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
 [0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0],
 [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0],
 [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0],
 [1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0],
 [0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1]]
[[1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0],
 [0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0],
 [0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0],
 [0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0],
 [0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1],
 [0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0],
 [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0],
 [0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0],
 [0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0]]
4 は 2.0 の2乗
16 は 4.0 の2乗
9 は 3.0 の2乗
100 は 10.0 の2乗
36 は 6.0 の2乗

さて、このプログラムで少し不満なのが、0か1しか値をとらないのに1変数分のメモリを食っているところです。
そこで各行を2進法のbit列とみて、1つの変数で表すことにします。このようにするとメモリの節約になり、Gauss消去の箇所にbit XORが使えるようになります。

# -*- coding: utf-8 -*-

from math import sqrt

# 「nをplistの素数で素因数分解したときの、各素数のべき乗の偶奇」をbitとして低位桁より並べた整数を返す
# 素因数分解できなければNoneを返す
def factoring_vector(n, plist):
    ans = 0
    for i,p in enumerate(plist):
        while n%p==0:
            n //= p
            ans ^= 1<<i
    if n!=1:
        return None
    return ans

# nのkビット目(0-indexed)
def bit(n, k):
    return (n>>k) & 1

# bit列を逆順にした文字列（出力用）
def bin_reverse(n, k):
    return format(n, 'b')[::-1].ljust(k,'0')

# Gauss消去
def gaussian_elimination(mat, row, col):

    for j in range(col):
        for i in range(j,row):
            if bit(mat[i],j) == 1:
                pivot_row = i
                break
        else:
            continue
    
        if pivot_row != j:
            mat[pivot_row],mat[j] = mat[j],mat[pivot_row]
            pivot_row = j
            
        for i in range(pivot_row+1, row):
            if bit(mat[i],j)==1:
                mat[i] ^= mat[j]                
    

if __name__ == '__main__':
    plist = [2,3,5,7,11]
    rlist = [2,3,4,5,6,7,8,9,10,11]
    mat = []
    
    
    for k,r in enumerate(rlist):
        v = factoring_vector(r, plist)
        if v is None:
            continue
        
        # 単位行列のk行目
        identity = 1 << k
        mat.append(v + (identity << len(plist)))
    
    for v in mat:
        print(bin_reverse(v, len(plist)+len(rlist)))

    
    # Gauss消去
    row = len(mat)
    col = len(plist)
    
    gaussian_elimination(mat, row, col)
    
    
    print("-----------")            
    for v in mat:
        print(bin_reverse(v, len(plist)+len(rlist)))
    
    for i in range(row):
        if (mat[i] & ((1<<col)-1)) > 0:
            continue
    
        n=1
        for j in range(len(rlist)):
            if bit(mat[i],col+j) == 1:
                n *= rlist[j]
        if n!=1:
            print(n,"は",sqrt(n),"の2乗")

100001000000000
010000100000000
000000010000000
001000001000000
110000000100000
000100000010000
100000000001000
000000000000100
101000000000010
000010000000001
-----------
100001000000000
010000100000000
001000001000000
000100000010000
000010000000001
000000010000000
000001000001000
000000000000100
000001001000010
000001100100000
4 は 2.0 の2乗
16 は 4.0 の2乗
9 は 3.0 の2乗
100 は 10.0 の2乗
36 は 6.0 の2乗

「ふるい」とは？

さて、問題をもう一度振り返ると、 $x$ を動かして $x^2$ を $N$ で割った余り $r$ をたくさん考え、いくつかの $r$ をうまく組合せて平方数を作るのでした。
$x^2 \equiv r \pmod{N}$

$r$ は小さい方が平方数が作りやすいため、 $x$ は $\sqrt{N}$ の近くで動かすこととしますが、やみくもに動かしても $r$ を素因数分解したときに多数の素数が出てきて効率が悪くなります。
上の例でいうと $11$ は１度しか出てこないため、平方数を作るのに貢献していません。

そこでまずある $m$ を決めて、 $m$ 個の素数 $p_1, p_2, \cdots, p_m$ を決め、これらで分解される $r$ のみを抽出することを考えます。
（ $p$ は $2$ または $N$ が平方剰余となる奇素数）

$x$ を動かしていった際に、 $x^2-N$ の中で素数 $p$ で割り切れるものがどこに現れるかを考えます。
$x^2\equiv N \pmod{p}$ の解を $x\equiv \pm t_p \pmod{p}$ と計算さえすれば、 $p$ 毎に $p$ の倍数が現れることがわかります。

この部分が2次「ふるい」法と呼ばれるゆえんで、エラトステネスの篩のようなプロセスで篩にかけて抽出していきます。

$p_1, p_2, \cdots, p_m$ 以外では割れない $r$ を求めたいので、最初に $w_i=\log{r_i}$ を計算し、 $p$ で割り切れれば $\log{p}$ を引いていき、 $0$ になれば $p_1, p_2, \cdots, p_m$ のみで割り切れるということになります。

小さい素数 $p$ の場合には、 $p^a$ で割り切れることも多いですが、 $p$ が奇素数の場合には、同様に1つの解を計算すれば $p^a$ 毎に割り切れます。

[木田]では素数のべきで割れるケースは無視して、 $\log{}$ がある閾値よりも低くなるときに実際に割り算して確かめる、という方法をとっています。実装上はこの方が楽だと思います。

# -*- coding: utf-8 -*-
from math import sqrt, exp, log

def isprime(n):
    if n<2:
        return False
    elif n==2 or n==3:
        return True
    elif n%2==0:
        return False
    else:
        i = 3
        while i*i <= n:
            if n%i == 0:
                return False
            i+=2
    return True   

# Legendre記号
# p: 素数
def legendre(a, p):
    # p=2のときは1を返しておく
    if(p==2): return 1
    # 奇素数の場合
    ret = pow(a, (p-1)//2, p)
#    print(a,p,ret)
    if ret==1:
        return 1
    else:
        return -1
        
# x^2 ≡ n (mod p)の解の1つを返す
def modsqrt(n, p):
    for i in range(p//2+1):
        if((i*i -n)%p==0):
            return i
    
    return None

# 「nをplistの素数で素因数分解したときの、各素数のべき乗の偶奇」をbitとして低位桁より並べた整数を返す
# 素因数分解できなければNoneを返す
def factoring_vector(n, plist):
    ans = 0
    for i,p in enumerate(plist):
        while n%p==0:
            n //= p
            ans ^= 1<<i
    if n!=1:
        return None
    return ans

# nのkビット目(0-indexed)
def bit(n, k):
    return (n>>k) & 1

# bit列を逆順にした文字列（出力用）
def bin_reverse(n, k):
    return format(n, 'b')[::-1].ljust(k,'0')

# Gauss消去
def gaussian_elimination(mat, row, col):

    for j in range(col):
        for i in range(j,row):
            if bit(mat[i],j) == 1:
                pivot_row = i
                break
        else:
            continue
    
        if pivot_row != j:
            mat[pivot_row],mat[j] = mat[j],mat[pivot_row]
            pivot_row = j
        
        for i in range(pivot_row+1, row):
            if bit(mat[i],j)==1:
                mat[i] ^= mat[j]
    
def gcd(a, b):
    if a<b:
        return gcd(b,a)
    r = b
    while a%b!=0:
        r = a%b
        a,b = b, r
    return r

def factoring(n):
    ret = []
    p=1
    while p*p<=n:
        p+=1
        if n%p!=0:
            continue
        num = 0
        while n%p==0:
            num+=1
            n //= p
        
        ret.append((p,num))

    if n!=1:
        ret.append((n,1))

    return ret            

    
if __name__ == '__main__':
    
    N = 8800969069 
    S = int(sqrt(N))+1
    kosuP = max(5, int(1.8*exp(sqrt(log(N)*log(log(N))/12))))
    print("kosuP=",kosuP)
    kosuX = int(kosuP*1.1)+4
    print("kosuX=", kosuX)

    # 素数列挙
    plist = [2]
    p = 3
    while True:
        if isprime(p) and legendre(N,p)==1:    
            if len(plist)==kosuP:
                break
            plist.append(p)

        p+=2
    
    
    # max_iは決め打ちとしている。実際にはkosuX個見つかるまで続ける必要あり
    max_i = 1000000
    work = [0] * max_i
    for i in range(max_i):
        work[i] = log((S+i)**2 - N)
        
    for p in plist:
        logp = log(p)
        
        root = modsqrt(N,p)
        for t in ([root, p-root] if p!=2 else [root]):            
            a = (t-S) % p
        
            assert(((S+a)**2 - N)%p == 0)
        
            while a < max_i:
                work[a] -= logp
                a += p

    mat = []
    rlist = []
    for i,w in enumerate(work):
        if w < 3.0:
            r = (S+i)**2 - N
            v = factoring_vector(r, plist)
            if v is None:
                continue

            # 単位行列のk行目
            identity = 1 << len(mat)
            mat.append(v + (identity << len(plist)))

            rlist.append(i)
            
            if len(mat) >= kosuX:
                break
        
    for v,r in zip(mat,rlist):
        print(bin_reverse(v, len(plist)+len(mat)))

    # Gauss消去
    row = len(mat)
    col = len(plist)
    
    gaussian_elimination(mat, row, col)
    
    
    print("-----------")            
    for v in mat:
        print(bin_reverse(v, len(plist)+len(mat)))    
    
    for i in range(row):
        if (mat[i] & ((1<<col)-1)) > 0:
            continue
    
        y2 = 1
        x2 = 1
        for j in range(len(rlist)):
            if bit(mat[i],col+j) == 1:
                y2 *= (S+rlist[j])**2 - N
                x2 *= S+rlist[j]
        if y2!=1:
            y = int(sqrt(y2)+0.5)
            #print(y2,"は",y,"の2乗")
            
            if gcd(x2+y,N) * (N//gcd(x2+y,N)) == N:
                print("divisor=",gcd(x2+y,N), N//gcd(x2+y,N))

kosuP= 20
kosuX= 26
0100001010000100000010000000000000000000000000
0001010010000000000101000000000000000000000000
0100000000100000011000100000000000000000000000
0011000100000000101000010000000000000000000000
0100010100100010000000001000000000000000000000
0010100001010001000000000100000000000000000000
0101100110001000000000000010000000000000000000
0010001100100100000000000001000000000000000000
0110100100000000110000000000100000000000000000
0011000001010000000100000000010000000000000000
0110011000100001000000000000001000000000000000
0010100000100100000100000000000100000000000000
0100100000000100001000000000000010000000000000
0110011000001000100000000000000001000000000000
0100100011001100000000000000000000100000000000
0000000001010010010000000000000000010000000000
0011101011000000000000000000000000001000000000
0010100001010001000000000000000000000100000000
0011000110100000100000000000000000000010000000
0011001000000000010100000000000000000001000000
0010111000101000000000000000000000000000100000
0110000010001001000000000000000000000000010000
0100110100001000000100000000000000000000001000
0101101000100000100000000000000000000000000100
0000111010000000001000000000000000000000000010
0011001000011010000000000000000000000000000001
-----------
0100001010000100000010000000000000000000000000
0100000000100000011000100000000000000000000000
0011000100000000101000010000000000000000000000
0001010010000000000101000000000000000000000000
0000110111010001101101010100000000000000000000
0000010100000010011000101000000000000000000000
0000001110100110110101111001000000000000000000
0000000101110001101000100100100000000000000000
0000000011111001110000110110000000000000000000
0000000001110101000100000100000100000000000000
0000000000100111000000001001001000000000000000
0000000000011000101101010101001000100000000000
0000000000001110010101101010000010000000000000
0000000000000110000100111101111000000000000000
0000000000000011101101111100110110000010000000
0000000000000001010101000111111100000010010000
0000000000000000110101000110111100101000000000
0000000000000000010100001101001100010000000000
0000000000000000000000100101111111101000000000
0000000000000000000101000100111000000011000000
0000000000000000000000010100111010101001100000
0000000000000000000000000100000000000100000000
0000000000000000000001000010000000000000001000
0000000000000000000000010001000010000000000100
0000000000000000000000110111111110101000000010
0000000000000000000001101110000010100001010001
divisor= 1 8800969069
divisor= 1 8800969069
divisor= 94349 93281
divisor= 1 8800969069
divisor= 1 8800969069
divisor= 1 8800969069
divisor= 1 8800969069

参考文献

[木田] 木田祐司, 牧野潔夫, UBASICによるコンピュータ整数論, 日本評論社, 1994

2019-04-14

Pythonで機械設計を自動化した話

仕事でとある機械を設計する仕事をしていました。
3年前ぐらいに設計をPythonで自動化した経験について書きます。

入社したときから設計に配属され、ずっと設計をしていました。
内製の多数の設計ツールを駆使して、手作業でひたすら計算して、設計クライテリアを満たす解を探したりして、最終的に2次元CADを作成します。
ツールだけ見るとかなり古臭いです。実際、インターフェースだけは変わったものの、10*n年前から使われているツールが当たり前という環境です。

手作業での作業は楽しくはあり、設計しているという実感を得られるものの、非常に非効率です。
入社当時は長時間残業が当たり前。
設計者は設計以外の雑用にも追われ、設計に取られる時間も限られています。
そんな中で手作業で計算をしているため、設計の最適解は当然のように得られず、もどかしさを感じていました。

設計というのは、ある制約条件下で何らかの最適解を求める作業です。
開発品で初めての製品を設計するならいざ知らず、類似品を多数設計するのであればプログラムで自動化して最適化すべきものです。

入社N年目に当時の課長に自動化を専任でやらせて欲しいと直訴し、専任でやらせてもらえることになりました。
（なぜあっさりやらせてもらえたのかという背景があるのですが、それはまた別の話。）

私の設計業務は基本設計だったので、内製の計算ツールを複数使い、形状を決定して、2次元CADで計画図を作成するのが主な業務です。（他にも雑務的な仕事は数知れず）
概算計画でも、計算慣れしているベテラン勢で１週間ぐらい、そこまで慣れていない若い人では２週間程度がかかるものです。
実際にはこのあとデザインレビューを行い、正式に図面や図書を発行する流れとなり、案件にもよりますが１ヶ月半～２カ月ぐらいかけるのが普通です。

受注の引合いがあったときの見積り設計は期限が短く、数日で概算設計を終わらせる必要がありました。入札に関わる重要なプロセスにも関わらず、あまり検討をしていない設計で応札するということも多かったです。これでは受注も遠ざかるばかりで、これは改善しなければ、という気持ちでした。

具体的な話

さて、どういう設計を手作業でしていたのかを説明していきます。
設計ツールはいろいろあって

性能計算ツール（GUI）
強度計算ツール（GUI、Excelシート）
○○計算ツール（Excelマクロツール）

のような感じ20個近いツールがあります。
さらにExcelマクロから呼び出すDLLもあります。

GUIと書いているものは、GUIはフロントエンドだけで、実際にはサーバのFortranプログラムを呼び出しています。
具体的にはGUIから入力テキストファイルを出力し、それをサーバにアップロードし、Fortranプログラムを走らせ、出力されたテキストファイルをダウンロードしています。

Excelシートでの計算ツールや、Excelのマクロを使ったツールがあるのは、他の設計現場でもよくあるのではないでしょうか？

実際の設計では例えば以下のような作業をします。

計算ツールＡの出力から数値をぬきだし、計算ツールBに入力する
計算ツールCの出力のある数値が制約以下になるような入力を探す

サーバのプログラムを走らせたり、Excelを使ったりと設計ツールが多岐に渡りますが、これらを自動的に走らせるのはPythonが向いています。C++とかに手を出すと死亡します。
既存の設計プログラムには一切手を加えず、Pythonでプログラム間の操作を仲介するような方針にしました。

Excelの操作の自動化

Excelの操作にはPythonのwin32comモジュールを使いました。
他にも色々なモジュールがあるようですが、特に比較検討をしたわけではないので、今はもっと良いものがあるのかもしれません。
ほとんどExcelマクロのVBAを書くのと同じ感覚で書くことができます。
PythonからExcelマクロを呼び出すこともできます。
Excelファイルを開いて、セルに数字を入力して、マクロを走らせて、数値を読みだして、ファイルを閉じる、といった作業がPythonから出来ます。
なお注意点として、PythonプログラムからExcelを操作している間にExcelを触ると、エラーで終了してしまうのが地味に不便でした。

サーバプログラムの呼び出しの自動化

これは完全に職場固有の問題なので、あまり参考にならないと思います。
多くの設計ツールがFortranプログラムとしてサーバ内にあるため、GUIプログラムからサーバのプログラムを呼び出して、出力をダウンロードするという処理になっていました。

ここをPythonから自動で行うには、主に以下の3つの関数を実装することになります。

計算の入力ファイルをファイルに書き出す関数
計算を走らせる関数
出力ファイルを変数に読みだす関数

計算はftpでアップロード、ダウンロードして、社内ネットワークなのでtelnetで入ってコマンドを叩く方法としました。これらは全てPythonのモジュールでできます。
出力ファイルを読み込むのは、欲しい数値が固定位置にあるとは限らないので、正規表現で読みだすことにしました。Pythonには正規表現が扱えるモジュールが最初から使えるので便利です。

最適化

設計計算をしていると、例えば出力されたある値が最小（最大）になるような入力値を探したいということがあります。
地道にループで書いてもいいのですが、scipy.optimizeという最適化に使えるモジュールがあるため、これが使えそうな処理であれば使うと楽です。

ログ出力

自動化プログラムを開発するうえで、ログ出力をするとデバッグに便利です。途中でエラーで止まったときにどこに不具合があるか特定しやすいです。
デバッグだけではなく、計算過程を出力しておくことで、あとでなぜその設計になったのかが確認できます。
loggingモジュールがあるので、これを使います。ちょっと使い方にコツがいるので調べてね。

ほかにもデバッグとしては、エラーで止まったときに、「import pdb; pdb.pm()」をやったりとか、あやしそうな箇所で「pdb.set_trace()」したりとかが有効です。

ログの一種としてグラフで経過をわかるようにもしました。matplotlibというグラフを表示するモジュールがあるため、非常に簡単にグラフを表示することができます。

AutoCADの作図の自動化

AutoCADでの作図にはAcadRemoconというフリーソフトを用いました。これはActiveX DLLで、AutoCADに作図コマンドを送ることができます。このActiveX DLLをPythonから呼び出すことで、AutoCADに作図コマンドを送り作図を行うことができます。
私の環境では問題なく動いているのですが、新しいバージョンのWindowsやAutoCADだとサポートされていないようなので、動くかどうかは保証できません。
もしAcadRemoconが使えないような環境であれば、AutoCADの作図コマンドをファイル出力して、ユーザがAutoCADのコマンドウィンドウに貼り付けることで作図できると思います。

作図コマンドで出来ることに限るため、あらゆる作図処理が出来るわけではないと思いますが、線や円弧を作図したり、レイヤーを変えたり、簡単な寸法を入れるぐらいであれば問題なく作図できます。
外部のdxfファイルにある図形を貼り付けるようなこともできます。これはおそらく線分や円弧などのエンティティ毎に貼り付ける操作を実装するしかないはず。少なくとも私はそれ以外は知りません。
このあたりは複雑な処理を行いたければ、AutoCAD.NET等でDLLを開発して、AutoCADからロードすれば出来ますが、資料が少ないのが難点ですね。和書が１冊出てた記憶です。

・AutoCAD作図のPythonプログラムのサンプル

何が出来たのか

自動化プログラムを開発することで、1週間ほどかかっていた計算が30分ほどで出来るようになりました。
実際のところ、設計自体が複雑でパラメータも多いため、全体を最適化までは出来なかったのですが、全体をワンフローで流し、一部のプロセスに限っては最適化することはできました。

副次的な効果として、以下のようなこともできました。

設計ルールが明文化されていない箇所が少なからずあり、ルールを決めることができた（というか決めなければ進められなかった）
自動化すると計算ミスが無くなった（もちろん最初の検証作業は必要。検証作業で大量のバグが見つかります）
自動化すると人の技量による差がなくなる（ベテランも新人も入力が同じなら同じ答えが出てくる）

なぜ開発がうまくいったのか

この手のプロジェクトは失敗がよくあると思います。
今回は開発がうまくいった例なのですが、一番の理由は設計をよく理解している人間がプログラムを書いたことです。
プログラムを動かして結果やインターフェースがイマイチだったときには、すぐに仕様を変更することができます。
これが外注に頼むと仕様を作りこむだけで数カ月、開発に数カ月、それだけかけてプログラムを動かしてみると期待していた結果が出てこないということになっていたはずです。こうなると追加で開発するために数百万がかかってきます。
設計にもよりますが、今回のような複雑な設計の場合、最初から仕様を固めるのは非常に難しいため、開発しながら考え、柔軟に方針転換ができます。新たなアイディアが思いついたときにも、すぐにプログラムを書き手元で試せます。

結論：設計者にプログラムを書かせよう

おしまい。

2019-01-20

素因数分解(2) p-1法、p+1法、楕円曲線法

数学

前回の記事（素因数分解(1) Pollardのρ法 - wacchoz’s note）でちらっと書きましたが、素因数分解のアルゴリズムは大きなカテゴリーが２つあり、そのうちの１つに $p-1$ 法、 $p+1$ 法、楕円曲線法が属しています。
今回はそれらについて書いていきます。

素因数分解(1) Pollardのρ法 - wacchoz’s note
素因数分解(2) p-1法、p+1法、楕円曲線法 - wacchoz’s note（今ここ）
素因数分解(3) フェルマー法、２次ふるい法 - wacchoz’s note

概要
p-1法
- Pythonによる実装
p+1法
楕円曲線法
- アルゴリズム
- Pythonによる実装
参考文献

概要

簡単に概要だけ説明すると、 $p-1$ 法は、 $(a,p)\neq 1$ のとき、
$\displaystyle a^{p-1}\equiv 1 \quad(\text{mod } p)$
となることから、約数の多い $M$ をとり（具体的には小さな素因数の積とし）、 $M$ が $p-1$ の倍数となっていれば、
$\text{gcd}(a^M-1, N)$ は $p$ の倍数となり、たいていの場合は $p$ そのものが見つかります。
この方法は $p-1$ が小さな素因数の積になっている場合に、素因数が見つかります。

$p+1$ 法も類似した方法で、 $p+1$ が小さな素因数の積になっている場合に、素因数が見つかる方法です。
ある数列を計算すると
$\displaystyle y_{p+1}\equiv 0\quad(\text{mod } p)$
となるため、約数の多い $M$ をとり、 $M$ が $p+1$ の倍数となっていれば、
$\text{gcd}(y_M, N)$ は $p$ の倍数となり、たいていの場合は $p$ そのものが見つかります。

これらは $p-1$ や $p+1$ が小さな素因数の積になっていないとうまくいかず、そうでなければ、 $M$ をひたすら大きくしていかなければ素因数が見つかりません。

楕円曲線法ではその欠点を克服しています。
$\displaystyle y^2\equiv x^3+ax+b\quad(\text{mod } p)$
で定まる楕円曲線 $E(a,b;p)$ の有理点の集合は、ある演算に対してアーベル群となります。
ここで、群の位数は $a, b$ を変化させると、様々な値をとります。
Hasseによって $\displaystyle p+1-2\sqrt{p}\le \#E(a,b;p) \le p+1+2\sqrt{p}$ が証明されていますし、 $a, b$ を変化させると、この範囲の整数値をすべて取りうることがDeuringにより証明されています。
ここで、 $m=\#E(a,b;p)$ と書くと、 $E(a,b;p)$ 上の点 $P$ に対して、 $mP=\mathcal{O}$ が成り立ちます。
したがって $M$ を小さな素数の積として選び、 $MP=\mathcal{O}$ が成り立てば、素因数が見つかります。

$p-1$ 法や $p+1$ 法は $p-1$ や $p+1$ が小さな素因数の積になっていないとうまくいかず、そうでなければ、 $M$ をひたすら大きくしていかなければ素因数が見つかりませんでした。楕円曲線法では $a, b$ を振ることで群の位数を変化させることができ、それらの中には小さな素因数の積になっているものもある可能性があり、 $p-1$ 法や $p+1$ 法よりも素因数が見つかる可能性が高くなっています。

p-1法

上の概要でほぼ語りつくしてしまった感じですが、実装までやってみたいと思います。

整数 $N$ の素因子の1つが $p$ だったとします。
$(a,p)\neq 1$ のとき、
$\displaystyle a^{p-1}\equiv 1 \quad(\text{mod } p)$
となることから、 $M$ を $p-1$ の倍数とすると
$\displaystyle a^M\equiv 1 \quad(\text{mod } p)$
が成り立ちます。
つまり $a^M-1$ が $p$ の倍数となるので、 $\text{gcd}(a^M-1, N)$ は $p$ の倍数となり、たいていの場合、素因子 $p$ が見つかります。

問題は $M$ をどのようにとるかですが、 $p$ が不明なので、 $p-1$ の倍数も当然不明です。そこで $M$ としては約数のできるだけ多い数であれば、素因数分解できる可能性が高くなると考えます。大きさの割に約数が多いものとなると、たくさんの小さな素数の積ということになります。

具体的にはある限界 $L$ を決めて、 $L$ 以下の素数のべきをすべて掛け合わせたものとします。
$\displaystyle M=\prod_{p=\text{prime}} p^{e_p} \quad \text{,where } p^{e_p}\le L < p^{e_p+1}$

$L$ は計算時間との兼ね合いになりますが、できるだけ大きめにとります。

Pythonによる実装

以下の実装は『UBASICによるコンピュータ整数論』（日本評論社）を参考にしています。
$M$ が非常に大きくなってしまうので、 $a^M$ を一気に計算せずに、 $p^{e_p}$ ごとに計算しています。

from math import  gcd   # version>=3.5

def isprime(n):
    if n<2:
        return False
    elif n==2 or n==3:
        return True
    elif n%2==0:
        return False
    else:
        i = 3
        while i*i <= n:
            if n%i == 0:
                return False
            i+=2
    return True       


if __name__ == '__main__':

    N = 2885500349

    L=1000
    a=2
    aM = 2
    for p in range(2,L+1):
        if not isprime(p):
            continue
        Mp = p
        while Mp*p <= L:
            Mp*=p
        #a^m mod Nの計算（素数pごとに計算）
        aM = pow(aM, Mp, N)

    g = gcd(aM-1, N)
    print(g)

実行するとわかりますが、 $L$ が小さいと答えが1になり素因数が見つかりません。
実装はしませんが、1になったら $L$ を大きくしていく必要があります。
また大きすぎて全ての素因子 $p$ に対して $\displaystyle a^M\equiv 1 \quad(\text{mod } p)$ が成り立つと、 $\displaystyle a^M\equiv 1 \quad(\text{mod } N)$ になってしまうので、その場合は答えが0になってしまいますので、 $L$ を小さくする必要があるはず。

$p-1$ 法では $p-1$ が小さな素数の積になっていないときはうまくいきませんが、（小さな素数の積）×（ちょっと大きな素数）ぐらいならなんとかなります。（ちょっと大きな素数）を $q$ とすると、同様に $\text{gcd}((a^M)^q-1, N)$ が素因数となる可能性が高い。 $q$ も適当な上限を決め、 $q$ が小さい方から順々に $\text{gcd}((a^M)^q-1, N)$ を計算していきます。 $q$ を増やす時には、べき乗の計算は差分だけにすれば良いです。

前半部を1st step、後半部を2nd stepと呼びます。これは $p+1$ 法でも同じようなことが出来ます。

2nd stepまでやっても、 $p-1$ に大きな素因子が複数あったり、1つの素因子であってもそれが巨大すぎる場合にはお手上げです。

p+1法

この方法は $p+1$ が小さな素数の積になっているときにうまくいく方法です。
以下の説明は『コンピュータと素因子分解』（和田秀男, 遊星社）によります。

$(N, b(a^2+4b))=1$ なる $a,b$ を選び、以下の数列を定義します。

$\displaystyle y_0=0, \quad y_1=1, \quad y_{i+1}=ay_i+by_{i-1}$

$x^2-ax-b=0$ の判別式を $d=a^2+4b$ , 2根 $\alpha, \beta$ を $\alpha=\frac{a+\sqrt{d}}{2}$ , $\beta=\frac{a-\sqrt{d}}{2}$ とおくと、

$\displaystyle y_n=(\alpha^n-\beta^n)/\sqrt{d}$

が成り立ちます。

同様に

$\displaystyle x_0=2, \quad x_1=a, \quad x_{i+1}=ax_i+bx_{i-1}$

と定めると
$\displaystyle x_n=\alpha^n+\beta^n$
となる。

単純な計算から

$\displaystyle x_n = y_{n+1} + by_{n-1}$

が示せる。

二項定理を用いると

$\displaystyle y_n=\frac{1}{2^{n-1}}\sum {}_nC_{2k+1} a^{n-2k-1}d^k$

$\displaystyle x_n=\frac{1}{2^{n-1}}\sum {}_nC_{2k} a^{n-2k}d^k$

となり、 $p$ を素数とすると

$\displaystyle 2^{p-1} y_p= \sum {}_pC_{2k+1} a^{p-2k-1}d^k \equiv d^{(p-1)/2} \quad(\text{mod }p)$

$\displaystyle 2^{p-1} x_p= \sum {}_pC_{2k} a^{p-2k}d^k \equiv a^p \equiv a \quad(\text{mod }p)$

となります。まず、 $x_p\equiv a$ です。
$d^{(p-1)/2}$ は $d$ が $\text{mod }p$ で平方剰余かどうかによって、 $d^{(p-1)/2} \equiv \pm 1\quad(\text{mod }p)$ となります。
仮に $d^{(p-1)/2}\equiv -1\quad(\text{mod }p)$ とすると、 $y_p\equiv -1$ となるため、

$\displaystyle y_{p+1} = ay_p + by_{p-1} \equiv -a + (x_p - y_{p+1}) \equiv -y_{p+1}$
となり
$\displaystyle y_{p+1} \equiv 0 \quad (\text{mod } p)$
となります。

同様に、仮に $d^{(p-1)/2}\equiv 1\quad(\text{mod }p)$ とすると、 $y_p\equiv 1$ となるため、

$\displaystyle by_{p-1} = y_{p+1}-ay_p = (x_p-by_{p-1})-ay_p \equiv -by_{p-1}$
となり
$\displaystyle y_{p-1}\equiv 0\quad(\text{mod }p)$
となります。

まとめると、 $d=a^2+4b$ が $\text{mod }p$ で平方剰余かどうかによって $y_{p-1}\equiv 0(\text{mod }p)$ または $y_{p+1}\equiv 0(\text{mod }p)$ が成り立ちます。

ここでp-1法と同様に $M$ を小さな素数の積とします。
例えば、 $y_{p+1}\equiv 0(\text{mod }p)$ が成立しているとすると、 $p+1$ が $M$ の約数であれば $y_M\equiv 0(\text{mod }p)$ となり、 $\text{gcd}(y_M, N)$ が素因数となっている可能性が高いというわけです。
事前に $p$ が不明なため、 $d$ が $\text{mod }p$ で平方剰余かどうかはわからないので、もし $y_{p-1}\equiv 0(\text{mod }p)$ が成り立っていれば、p-1法と同じになってしまいます。（しかもp-1法よりも遅い）
したがって、 $a, b$ の組合せを何通りか試す必要があります。

さて大きな $M$ に対して $y_M$ を計算するにはどうすればいいでしょうか。

$\displaystyle y_{2n}=2y_n y_{n+1}-ay_n{}^2$
$\displaystyle y_{2n+1}=y_{n+1}{}^2 + by_n{}^2$
$\displaystyle y_{2n+2}=a y_{n+1}{}^2 + 2by_n y_{n+1}$

が成り立つため、繰り返し２乗法と同様の考え方で、 $O(\log{M})$ で計算できます。 $y_n, y_{n+1}$ のペアから $y_{2n}, y_{2n+1}$ または $y_{2n+1}, y_{2n+2}$ のペアに遷移できるためです。

楕円曲線法

楕円曲線の有理点が群をなすことについては、数論好きには有名事実なのですが、説明をするのがなかなか大変なので、tsujimotterさんの記事が非常によくまとまっているので、こちらを参照下さい。

tsujimotter.hatenablog.com
tsujimotter.hatenablog.com

Wikipediaにも結果だけならある程度書いてあります。
楕円曲線 - Wikipedia

$\text{gcd}(4a^3+27b^2, p)\neq 0$ となる $a, b$ に対し
$\displaystyle y^2 \equiv x^3+ax+b \quad(\text{mod }p)$
の解 $(x\text{ mod }p, y\text{ mod }p)$ の全体に無限遠点 $\mathcal{O}$ を追加した集合に対して、以下のように演算 $"+"$ を定義します。

2点 $P_1=(x_1, y_1), P_2=(x_2, y_2)$ に対して、 $P_3=P_1+P_2$ の座標 $(x_3, y_3)$ を、

$x_1\not\equiv x_2$ の場合、
$\displaystyle \lambda\equiv (y_2-y_1)/(x_2-x_1)$

$x_1\equiv x_2$ で $y_1\equiv y_2\not\equiv 0$ の場合、
$\displaystyle \lambda\equiv (3x_1{}^2+a)/2y_1$

とおき、
$\displaystyle x_3\equiv \lambda^2 - x_1 - x_2 \\ y_3\equiv \lambda (x_1-x_3)-y_1$
と定義します。

$x_1\equiv x_2$ で $y_1\equiv -y_2$ の場合、
$\displaystyle P_1+P_2 = \mathcal{O}$

と定義します。

これらの計算はすべて $\text{mod }p$ で計算します。（除算は逆元を掛けます）

これが群の定義を満たします。（結合法則の証明が面倒ですが）
この群を $E(a,b;p)$ と書くことにします。

$m=\#E(a,b;p)$ と書くと、 $E(a,b;p)$ 上の点 $P$ に対して、 $mP=\mathcal{O}$ が成り立ちます。
$mP$ は $P$ を $m$ 回加算することを意味します。

$M$ を $m$ の倍数とすると $MP=\mathcal{O}$ が成り立ちます。
ここからは $p-1$ 法と同じですが、ある限界 $L$ を決めて
$\displaystyle M=\prod_{p=\text{prime}} p^{e_p} \quad \text{,where } p^{e_p}\le L < p^{e_p+1}$
と定め、 $MP=\mathcal{O}$ が成り立つかどうかを調べていきます。

$a,b$ を動かすと、 $\displaystyle p+1-2\sqrt{p}\le \#E(a,b;p) \le p+1+2\sqrt{p}$ の範囲の整数値をすべてとります。
それらの中には小さな素数の積になっているものをありえます。これが $p-1$ 法にまさる理由です。
$p-1$ 法ではうまくいかないときに $M$ を大きくするしかありませんでした。
楕円曲線法ではうまくいかなければ、 $a,b$ を変えれば $\#E(a,b;p)$ が小さな素数の積になる可能性に期待できます。

具体例を考えていきます。
例として $p=17$ として、 $y^2\equiv x^3+2x+6 \quad(\text{mod }17)$ 上の点 $P=(1,3)$ を次々に $n$ 倍していくと次のようになり、11倍したところで $\mathcal{O}$ になります。

1*P = (1,3)
2*P = (2,16)
3*P = (13,11)
4*P = (11,13)
5*P = (6,9)
6*P = (6,8)
7*P = (11,4)
8*P = (13,6)
9*P = (2,1)
10*P = (1,14)
11*P = O

さて、 $\text{mod }p$ で話を進めてきましたが、実際には $\text{mod }N$ で計算することになります。もちろん $N$ が素因数分解したい数です。

環 $\mathbb{Z}/N\mathbb{Z}$ は体ではないので、必ずしも逆元を持つわけではありません。

上の例で考えていきます。 $N=17*19$ をmodとして計算すると以下のようになります。

1*P = (1,3)
2*P = (223,135)
3*P = (13,147)
4*P = (130,64)
5*P = (193,94)
6*P = (57,280)
7*P = (215,242)
8*P = (200,57)
9*P = (291,290)
10*P = (171,252)

$11P=P+10P$ を計算しようとすると $\displaystyle \lambda\equiv (y_2-y_1)/(x_2-x_1)\equiv (252-3)/(171-1)$ を計算することになるが、 $171$ も $1$ もmod 17では合同であるため $N=17*19$ では逆元が存在しません。しかしながら $gcd(171-1, N)$ により素因数が見つかることになります。

つまり $\displaystyle \lambda\equiv (y_2-y_1)/(x_2-x_1)$ を計算する際に、 $\displaystyle \text{gcd}(x_2-x_1, N)=1$ であれば逆元をもち計算できますが、
$\displaystyle 1\lt\text{gcd}(x_2-x_1, N)\lt N$ であれば逆元が存在しません。しかしながら $\displaystyle \text{gcd}(x_2-x_1, N)$ は $N$ の非自明な約数であり、素因数分解できたことになります。
$\displaystyle \text{gcd}(x_2-x_1, N)=0$ のときは不運で、逆元の計算ができないうえに何も言えません。 $M$ を小さくして再計算するか、違う曲線から再スタートするかのどちらかとなります。

アルゴリズム

$N$ の大きさに合わせて $L$ を定め、 $\displaystyle M=\prod_{p=\text{prime}} p^{e_p} \quad \text{,where } p^{e_p}\le L < p^{e_p+1}$ とします。
$a, b$ をランダムにとります。
$y^2\equiv x^3+ax+b \text{ mod }N$ となる $(x, y)$ をとる。
点 $P=(x,y)$ に対しその $M$ 倍を計算します。もし途中で割り算の計算ができなくなれば、その分母から $N$ の約数が求まります。
もし $M$ 倍が計算できれば、別の $a, b$ から繰り返します。

なお実際には、ステップ2,3は、 $a, x, y$ をランダムにとってから、 $b$ を定めるように決めます。また計算には $b$ は使われないので求める必要もありません。

Pythonによる実装

例外を投げて答えを返すクソ実装なので、参考程度に。

from copy import copy
import math
from math import gcd  # version >= 3.5
import random

def isprime(n):
    if n<2:
        return False
    elif n==2 or n==3:
        return True
    elif n%2==0:
        return False
    else:
        i = 3
        while i*i <= n:
            if n%i == 0:
                return False
            i+=2
    return True       

def egcd(a, b):
    if a == 0:
        return (b, 0, 1)
    else:
        g, y, x = egcd(b % a, a)
        return (g, x - (b // a) * y, y)

# 例外送出用
class ModInvException(Exception):
    def __init__(self, x, string):
        self.x = x
        self.string = string

def modinv(a, m):
    a = a % m

    g, x, y = egcd(a, m)
    if g != 1:
        raise ModInvException(a, 'modular inverse does not exist. (%s,%s)' % (a,m))
    else:
        return x % m


class Point(object):
    a=0
    N=0
    
    def __init__(self, x=0, y=0):
        self.x = x
        self.y = y

    def set_curve(a, N):
        Point.a = a
        Point.N = N

    def __add__(self, right):
        
        if self.x != right.x:
            slope = (right.y-self.y) * modinv(right.x-self.x, self.N)
        elif self.x == right.x and self.y==right.y and self.y!=0:
            slope = (3*self.x**2 + Point.a) * modinv(2*self.y, self.N)
        else:
            raise Exception('result is O!')

        x3 = (slope**2-self.x - right.x) % self.N
        y3 = (slope * (self.x - x3) - self.y) % self.N

        return Point(x3, y3)

    def __mul__(self, right):
        if right<1:
            raise Exception("")

        r = right - 1
        result = copy(self)
        P = copy(self)
        while r > 0:
            if r%2==1:
                result = (result + P)
            P = P + P
            r = r//2
          
        return result

    def __repr__(self):
        return "(%s,%s)" % (self.x, self.y)



def elliptic_factorization(N):
    
    L=min(20000, int(1000*math.exp((math.log(math.sqrt(N))-21.8)*0.13))+100)
    print("L=",L)
    
    
    while True:
        a = random.randint(0,N)
        x = random.randint(0,N)
        y = random.randint(0,N)
        
        Point.set_curve(a,N)
        P = Point(x,y)
        for p in range(2,L+1):
            if not isprime(p):
                continue
            Mp = p
            while Mp*p <= L:
                Mp*=p

            try:
                # M*P mod Nの計算（素数pごとに計算）
                P = P * Mp
            except ModInvException as err:
                print(err.string)
                divisor = gcd(N, err.x)
                return divisor
            except:                
                continue


if __name__ == '__main__':

    N = 18**16+1
    
    divisor = elliptic_factorization(N)
            
    print("divisor=", divisor)
    if N == divisor * (N//divisor):
        print("%d = %d * %d" % (N, divisor, N//divisor))
    else:
        print("エラー")

出力例

L= 1287
modular inverse does not exist. (54602958734510002506,121439531096594251777)
divisor= 3930785153
121439531096594251777 = 3930785153 * 30894471809

参考文献

和田秀男, コンピュータと素因子分解, 遊星社, 1987
木田祐司, 牧野潔夫, UBASICによるコンピュータ整数論, 日本評論社, 1994
J.H.シルヴァーマン, J.テイト, 楕円曲線論入門, シュプリンガーフェアラーク東京, 1995

2019-01-05

素因数分解(1)　Pollardのρ法

数学

RSA暗号が素因数分解の難しさを安全性の根拠にしていることからわかる通り、大きな数の素因数分解は非常に難しいです。
今のところ、200桁程度の数の素因数分解が限界のようです。

素因数分解(1) Pollardのρ法 - wacchoz’s note（今ここ）
素因数分解(2) p-1法、p+1法、楕円曲線法 - wacchoz’s note
素因数分解(3) フェルマー法、２次ふるい法 - wacchoz’s note

素因数分解アルゴリズムはいくつかの方法が知られています。
ざっくり分けると

p-1法、p+1法、楕円曲線法
フェルマー法、２次ふるい法、数体ふるい法

の2つのカテゴリーになりますが、今回紹介するPollardのρ法は、どちらにも属しません。

Pollardのρ法は、1975年にポラードが考案した方法です。古典的な方法で、ある程度小さい素因子をもつ場合にしか適用できないものの、他のアルゴリズムとは一風変わった面白い手法です。
ポラード・ロー素因数分解法 - Wikipedia

まず素数 $p$ を適当に１つとり、
$a_1 = 2 \\ a_{i+1}=a_i^2+1 \quad\text{mod }p\quad(i=1,2,\cdots)$

と数列を定義すると、 $a_i$ は疑似乱数のように振る舞います。
$a_{i+1}=a_i^2+1$ の数式自体にあまり意味はなく、他の数式でも疑似乱数のように振る舞うものであれば、何でもOKです。

$a_i$ は $0$ から $p-1$ の値をとるため、いつか同じ値をとり、その後、周期的に変化することになります。

例として、 $p=131$ としてみると、

$2, 5, 26, 22, 92, 81, 12, 14, 66, 34, 109, 92,\cdots$

となり、12項目と5項目が一致しました。この後は周期7で繰り返すことになります。

100000までの素数で、何項目で初めて一致する値が出現するかをプロットしてみます。
f:id:wacchoz:20190104233620p:plain

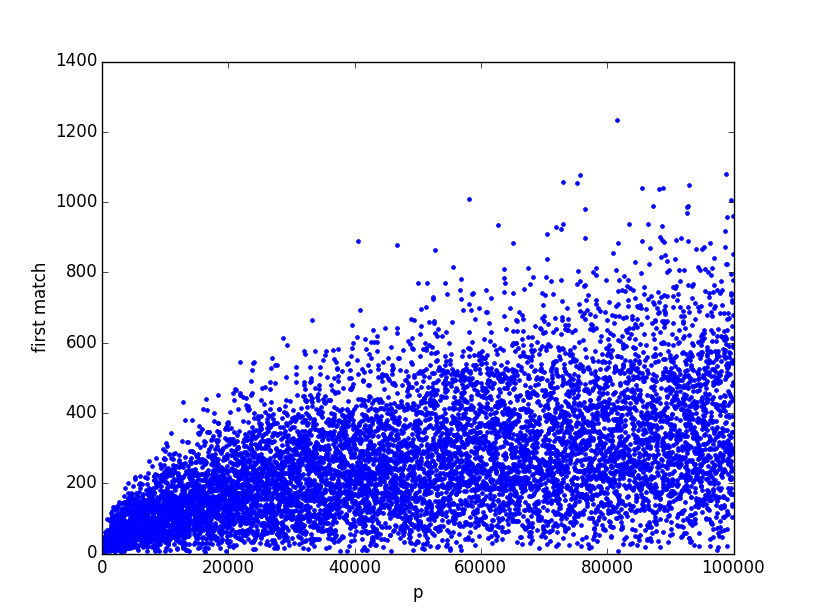
プロットしてみると、 $a_i$ は $0$ から $p-1$ の値をとりうるにもかかわらず、かなり早めに一致する値が出現することがわかります。
pが10^5ぐらいでも、数100項目で一致する値が出現します。

これに似た話は誕生日のパラドックスとしてよく知られています。
ランダムに23人を集めてきたら、その中に同じ誕生日の組がいる確率は50%を超え、70人いれば99.9%にも達します。

一般的には、 $n$ 通りの値をとる乱数があるとき、 $a$ 個の中に同じ値が出現する確率が50%を超えるのは、
$\displaystyle a\sim 1.1774\sqrt{n}$
で、 $n$ の値に比較して、かなり少ない個数で一致します。

さて、今までは素数 $p$ を法とした計算としていたが、素因数分解したい数 $N$ を法とした計算をしてみます。

$N=131\cdot 193=25283$ として、 $a_i$ を計算してみます。

$\displaystyle \begin{align} \text{mod }131& &\text{mod }25283 \\ 2 & & 2 \\ 5 & & 5 \\ 26 & & 26 \\ 22 & & 677 \\ \star 92 & & 3236 \\ 81 & &4535 \\ 12 & & 11147 \\ 14 & & 14948 \\ 66 & & 16834 \\ 34 & & 11693 \\ 109 & & 21069 \\ \star 92 & & 9131 \end{align}$
mod 25283の数列について、mod 131で考えると左側の数列と一致するので、9131と3236はmod 131で合同になるはずです。
実際、9131-3236は131で割りきれますし、 $N$ も131で割り切れるため、

$\text{gcd}(25283, 9131-3236) = 131$

となっています。そこで、

「合成数 $N$ が与えられたとき、 $a_k$ を計算時に、 $a_k-a_1, a_k-a_2, \cdots, a_k-a_{k-1}$ と $N$ との最大公約数を計算し、1でなければ終了。1であれば次のkに進む」

という方法が思いつきます。この方法は素因数を $p$ とすると、 $k=\sqrt{p}$ のオーダーまでにかなりの確率で素因子が見つかりますが、計算量が $k(k-1)/2$ に比例するため、結局のところ、 $p$ に比例する計算量となり、試し割り算と変わりません。

もっと効率的に計算するために、フロイドの循環検出法という手法を用います。
フロイドの循環検出法 - Wikipedia

ある $a_i$ から先は $a_i\equiv a_{i+K} \quad(\text{mod } p)$ となったとします。つまり数列のある箇所から先が周期 $K$ になったということです。
このとき、 $i\le K\cdot t$ になるように $t$ を大きくとると
$a_{Kt} \equiv a_{Kt+K} \equiv \cdots \equiv a_{Kt+Kt}$
となるため、 $m=K\cdot t$ とおくと
$a_{2m} \equiv a_m\quad(\text{mod } p)$
が成り立ちます。

ちなみに下図がρ法の名前の由来。
f:id:wacchoz:20190105225443p:plain:w240

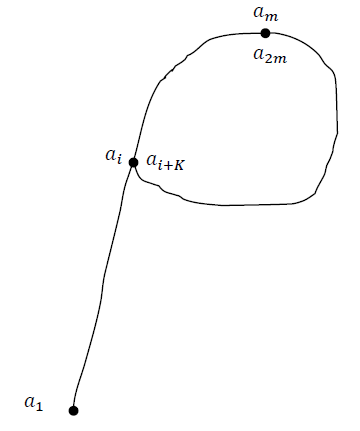
よって $1\lt \text{gcd}(a_{2m}-a_m, N) \lt N$ となる可能性が高く、そうなれば素因子が見つかったことになります。
$m$ の値はわからないため、小さい順に $a_{2k}-a_k$ を計算し、 $N$ との最大公約数をとります。

具体的には、2系統の数列 $(a_1, a_2, \cdots, a_k, \cdots)$ と $(a_2, a_4, \cdots, a_{2k}, \cdots)$ を生成し、順に $\text{gcd}(a_{2k}-a_k, N)$ を計算すればよいです。

計算量は平均的には $\sqrt{p}$ に比例となるため、 $O(N^{1/4})$ でおさえられます。

def gcd(a, b):
    if a<b:
        return gcd(b,a)
    r = b
    while a%b!=0:
        r = a%b
        a,b = b, r
    return r

def f(x):
    return x*x+1

N = 2**(2**6)+1 
print(N)
x=2
y=2
for i in range(10**7):
    x = f(x) % N
    y = f(f(y)) % N
    g = gcd(x-y, N)
    if 1<g<N:
        print(g)
        break
else:
    print("Fail")

参考文献

和田秀男, コンピュータと素因子分解, 遊星社, 1987
木田祐司, 牧野潔夫, UBASICによるコンピュータ整数論, 日本評論社, 1994

2018-12-28

APR-CL素数判定法

数学

APR-CL素数判定法(Adleman–Pomerance–Rumely-Cohen-Lenstra primality test, APR-CL primality test)について概説＆実装してみる。
この素数判定法はAdleman–Pomerance–Rumelyらによって開発された方法で、のちにCohenとLenstraによって改良されています。
数100桁程度の数に対しても現実的な時間で素数判定ができるすごいやつです。
ただし使う数学の道具も高度で、場合分けも多く、実装は重めです。確率的に「ほぼほぼ素数」と判定すればいいだけなら、Miller–Rabin法などを使う方が実装は楽です。

参考文献
Dirichlet指標とGauss和
Gauss和を用いた素数判定の原理
Jacobi和への書き換え
素数判定アルゴリズム
- 事前計算
- 素数判定
Python3による実装

参考文献

[APR] Adleman, Leonard M.; Pomerance, Carl; Rumely, Robert S. (1983). "On distinguishing prime numbers from composite numbers". Annals of Mathematics. 117 (1): 173–206.
[Coh-Len1] Cohen, Henri; Lenstra, Hendrik W., Jr. (1984). "Primality testing and Jacobi sums". Mathematics of Computation. 42 (165): 297–330.
[Coh-Len2] H. Cohen and A. K. Lenstra, Implementation of a new primality test. Math. Comp. 48 (1987), 103-121.
[和田] 和田秀男, コンピュータと素因子分解, 遊星社, 1987
[Cohen] H. Cohen, "A course in computational algebraic number theory". Springer-Verlag, Berlin, 1993
[Chmie] A Chmielowiec, "Primality proving with Gauss and Jacobi sums", 2004.

[APR]はおそらく読まなくても大丈夫。
[Coh-Len1]が[APR]からの改良です。
[Coh-Len2]も実装の上で有用なことが書いています。
和書でAPR法の解説をしているのは[和田]しか見たことがありません。ただ実装できるレベルまでの解説は無いので、実装するなら[Cohen]の本が良いかと思います。
[Chmie]は[Cohen]を簡潔にまとめた解説論文です。

Dirichlet指標とGauss和

まずDirichlet指標 $\chi$ とGauss和の導入をします。
乗法群 $(\mathbb{Z}/q\mathbb{Z})^\times$ から、（0でない）複素数全体の乗法群 $\mathbb{C}^\times$ への群準同型
$\displaystyle \chi : \mathbb{Z}/q\mathbb{Z}^\times\to \mathbb{C}^\times$
を素数 $q$ を法とするDirichlet指標と呼びます。
つまりmod $q$ での乗算構造をそのままに、複素数の乗法に置き換えたもの。
ディリクレ指標 - Wikipedia

具体的に指標の1つを構成します。
奇素数 $q$ の原始根の1つを $g$ とします。 $(a, q)\neq 1$ とすると
$\displaystyle a\equiv g^x (\text{mod } q)$
なる $x$ が $\text{mod } (q-1)$ で唯一に定まる。この $x$ を $\text{ind } a$ と表す。
イメージ的には $\log_g a$ のような対数。

$p$ を $q-1$ の素因子の1つとし、 $p^k \mid q-1$ であり $p^{k+1} \nmid q-1$ とします。
1の原始 $p^k$ 乗根を
$\displaystyle \zeta_{p^k}=e^{2\pi\sqrt{-1}/p^k}$
とすると、
$\displaystyle \chi(a) = \zeta_{p^k}{}^x =\zeta_{p^k}{}^{\text{ind }a}$
とすればDirichlet指標となっています。

あるいは以下のように書いた方が直感的でわかりやすいかも。
$\displaystyle \chi(g^x \text{ mod } q) = \zeta_{p^k}{}^x$

定義から
$\displaystyle \chi(ab)=\chi(a)\chi(b)$
が成立するのは明らかでしょう。

さてここで、Gauss和 $\tau(\chi)$ を
$\displaystyle \tau(\chi) = \sum_{x\in (\mathbb{Z}/q\mathbb{Z})^*} \chi(x) \zeta_q{}^x$
と定義します。

$\displaystyle \zeta_q^{q-1} + \zeta_q^{q-2} + \cdots + \zeta_q + 1 = 0$
$\displaystyle \zeta_{p^k}{}^{(p-1)p^{k-1}} + \zeta_{p^k}{}^{(p-2)p^{k-1}} + \cdots + \zeta_{p^k}{}^{p^{k-1}} + 1 = 0$
が成り立つため、Gauss和は
$\displaystyle \tau(\chi)=\sum_{i=0}^{(p-1)p^{k-1}-1} \sum_{j=0}^{q-2} a_{ij}\zeta_{p^k}{}^i\zeta_q{}^j$
という形に表せ、この形に表したときに $a_{ij}$ は一意に決まることが証明できる。
よって
$\displaystyle \sum_{i=0}^{(p-1)p^{k-1}-1} \sum_{j=0}^{q-2} a_{ij}\zeta_p{}^i\zeta_q{}^j \equiv \sum_{i=0}^{(p-1)p^{k-1}-1} \sum_{j=0}^{q-2} b_{ij}\zeta_p{}^i\zeta_q{}^j (\text{ mod } N)$
の意味を
$\text{すべての}i, j \text{に対して} a_{ij}\equiv b_{ij} (\text{mod }N)$
と定めてもいいです。

Gauss和を用いた素数判定の原理

具体的に話を進めるために
$t=5040=2^4 \cdot 3^2 \cdot 5 \cdot 7$
とする。 $q-1$ が $t$ の約数となる素数 $q$ はたくさんある。例えば
$11-1 = 2\times 5, \quad 43-1=2\times 3 \times 7$
であるので、 $11, 43$ などが $q$ の候補となる。
これらの $q$ についての積 $e(t)$ を
$\displaystyle e(t) = 2 \prod_{q \text{ is prime}, (q-1)\mid t} q^{v_q(t)+1}$
と定義する。ここで $v_q(t)$ は $t$ の素因子分解の中に $q$ が何回現れるかという回数である。

$t=5040$ のとき、
$\begin{eqnarray} e(t) &=& 2^6 \cdot 3^3 \cdot 5^2 \cdot 7^2 \cdot 11 \cdot 13\cdot 17\cdot 19\cdot 29\cdot 31\cdot 37\cdot 41\cdot 43\cdot 61\cdot 71\cdot 73\cdot 113\cdot 127\cdot 181\cdot 211\cdot 241\cdot 281\cdot 337\cdot 421\cdot 631\cdot 1009\cdot 2521\\ &=& 15321986788854443284662612735663611380010431225771200 \\ &\fallingdotseq& 1.53\times 10^{52} \end{eqnarray}$
となる。素数判定したい数を $N$ とすると、 $N\lt e(t)^2$ までの数が素数判定できる。
実装上は $e(t)$ はテーブルにしておき、条件を満たすtを探すことになる。

$N$ はあらかじめ試し割り算で小さな素因数は無いことがわかっているものとする。つまり、 $(N, t\cdot e(t))=1$ としてよい。

$q \mid e(t)$ なる $q$ を選び、さらに $p$ を $q-1$ の素因子の1つとし、 $p^k \mid q-1$ であり $p^{k+1} \nmid q-1$ とします。（最初の方のGauss和の説明と同じ記号にしています。）

このとき、 $N$ が素数であれば
$\displaystyle \begin{eqnarray} \tau(\chi)^N &=& \left( \sum \chi(x) \zeta_q{}^x \right)^N \\ & \equiv & \sum_x \chi(x)^N \zeta_q{}^{Nx} \\ & \equiv & \chi(N)^{-N} \sum_x \chi(Nx)^N \zeta_q{}^{Nx} \quad (\text{mod } N) \end{eqnarray}$
となる。 $x$ が $1$ から $q-1$ まで動けば、 $Nx$ も $1$ から $q-1$ まで動くので
$\displaystyle \begin{eqnarray} \tau(\chi)^N &\equiv& \chi(N)^{-N} \sum_x \chi(x)^N \zeta_q{}^{x} \quad (\text{mod } N) \\ &=& \chi(N)^{-N} \tau(\chi^N) \end{eqnarray}$
が成り立つ。

最後の
$\displaystyle \tau(\chi)^N \equiv \chi(N)^{-N} \tau(\chi^N) \quad (\text{mod } N)$
がポイントで、もしこの合同式が成立しなければ、 $N$ は合成数となる。
素数 $p, q$ の組合せは多数あるが、 $N$ が素数であれば、すべての組合せで成立しなければならず、一度でも成立しなければ合成数とわかる。
Fermatの小定理と考え方は同じ。

この合同式がすべての $p, q$ について成立しても、残念ながら素数とはいえず、次のステップに進むことになりますが、ひとまずそれは置いておきます。

この計算量を見積もってみます。 $N$ は100桁ぐらいを想定しておきます。 $p, q$ の組合せはいろいろありますが、一番大きいケースで $q=2521, p^k=3^2$ です。
Gauss和を
$\displaystyle \tau(\chi)=\sum_{i=0}^{(p-1)p^{k-1}-1} \sum_{j=0}^{q-2} a_{ij}\zeta_{p^k}{}^i\zeta_q{}^j$
と表したとき、メモリ量は $10^4$ のオーダーとなる。
Gauss和同士の積は、愚直に計算すると、その2乗となり $10^8$ 程度。
$\tau(\chi)^N$ の計算は繰り返し2乗法を使えるので、 $\log_2 N$ に比例する計算量であり、300回程度の繰り返しとなる。全体として $10^{10}$ となる。さらに $a_{ij}$ は $\text{mod } N$ で計算する必要があり、多倍長計算となる。
これを多数の $p, q$ の組合せについて計算するので、不可能ではないレベルだが、実用上は不満のある計算量となる。

これをJacobi和を用いた形に書き換えていく。

Jacobi和への書き換え

Gauss和を用いると計算量が増えるのは、Gauss和は $\mathbb{Z}\left[\zeta_q, \zeta_{p^k}\right]$ という大きな環に属していたことが原因といえる。
唐突だが、 $\chi_1$ と $\chi_2$ を $\text{mod }q$ でのDirichlet指標とするとき、 Jacobi和を
$\displaystyle j(\chi_1, \chi_2) = \sum_{x\in (\mathbb{Z}/q\mathbb{Z})^\times} \chi_1(x) \chi_2(1-x)$
と定義する。
このJacobi和は $\mathbb{Z}\left[\zeta_{p^k}\right]$ という小さな環に属しているので計算量が少ないです。先の例でいえば、 $p^k=2^4$ が最大である。

$\chi_0$ を $(x, q)=1$ のとき $\chi_0(x)=1$ 、それ以外のとき $\chi_0(x)=0$ となる自明な指標とする。
Jacobi和の性質として、以下が成り立つ。
(1) $\chi \neq \chi_0$ を $\text{mod }q$ のDirichlet指標とすると、
・ $\displaystyle \tau(\chi)\tau(\bar{\chi}) = \chi(-1)q$
・ $\displaystyle \left|\tau(\chi)\right| = \sqrt{q}$
(2) $\chi_1$ と $\chi_2$ を $\chi_1\chi_2\neq\chi_0$ なる $\text{mod }q$ のDirichlet指標とすると
・ $\displaystyle j(\chi_1, \chi_2) = \frac{\tau(\chi_1)\tau(\chi_2)}{\tau(\chi_1\chi_2)}$

例えば $p=5$ のとき
$\displaystyle \begin{eqnarray} \tau(\chi)^5 &=& (\tau(\chi)\cdot\tau(\chi))^2\cdot \tau(\chi) \\ &=& (j(\chi, \chi)\cdot\tau(\chi^2))^2\cdot \tau(\chi) \\ &=& j(\chi, \chi)^2\cdot j(\chi^2, \chi^2) \cdot \tau(\chi^4)\cdot \tau(\chi) \\ &=& j(\chi, \chi)^2\cdot j(\chi^2, \chi^2) \cdot \chi(-1)\cdot q \end{eqnarray}$
のようにJacobi和の積にできたりします。

新たな記号を導入します。
$(a,n)=1$ として、 $\sigma_a$ を $\sigma_a(\zeta_n)=\zeta_n{}^a$ とします。（ $\sigma_a \in \text{Gal}(\mathbb{Q}(\zeta_n))/\mathbb{Q}$ ）
$G=\{ \sigma_a: (a,n)=1, \sigma_a(\zeta_n)=\zeta_n{}^a \}$ とし、 $\sigma_a$ の整数係数の和からなる群環 $\mathbb{Z}[G]$ を定義します。
$f=\sum_{\sigma\in G} f_\sigma \sigma \quad (f_\sigma \in \mathbb{Z})$ と書くとき、
$f\in \mathbb{Z}[G]$ と $x\in \mathbb{Q}(\zeta_n)$ とするとき、 $f$ の $x$ への作用を、
$\displaystyle x^f=\prod_{\sigma\in G} \sigma(x)^{f_\sigma}$
で定義します。

少しわかりにくいですが、ただの表記だけの問題で、
$\displaystyle x^{2\sigma_a+3\sigma_b} = \sigma_a(x)^2\cdot \sigma_b(x)^3$
のように計算します。

素数判定式を以下のように言い換えます。
「 $\beta\in \mathbb{Z}[G]$ とするとき、 $N$ が素数であれば、1の $p^k$ 乗根 $\eta(\chi)$ が存在し、
$\displaystyle \tau(\chi)^{\beta(N-\sigma_N)} \equiv \eta(\chi)^{-\beta N}\quad (\text{mod }N)$
となる。」

ここからかなり技巧的に感じる式変形をします。
$a, b$ を $p \nmid ab(a+b)$ なる整数とし、 $E$ を $1\le x \lt p^k$ かつ $p\nmid x$ なる整数の集合とするとき、
$\displaystyle \alpha = \sum_{x\in E} \left\lfloor \frac{Nx}{p^k} \right\rfloor \sigma_x{}^{-1}$
と
$\displaystyle \beta = - \sum_{x\in E} \left( \left\lfloor \frac{xa}{p^k}\right\rfloor + \left\lfloor \frac{xb}{p^k}\right\rfloor - \left\lfloor \frac{x(a+b)}{p^k}\right\rfloor \right) \sigma_x{}^{-1}$
とすると、
$\displaystyle \tau(\chi)^{\beta(N-\sigma_N)} = j(\chi^a, \chi^b)^\alpha$
と変形でき、Gauss和がJacobi和に書き換えできました。

判定する際には、 $a=b=1$ をとります。ただし $p \nmid ab(a+b)$ という制約のため、 $p=2$ のときには場合分けが必要です。
ここから先の詳細は[Cohen]か[Coh-Len1]を参照ということで。

素数判定アルゴリズム

[Cohen]に従い、実際に実装できるレベルでアルゴリズムをまとめておきます。

事前計算

Jacobi和などを事前計算しておきます。
$B$ を素数判定したい数の上限とします。
このステップは $B$ のみにより、素数判定したい数 $N$ にはよりません。

$e(t)^2>B$ となる $t$ を見つける。
$e(t)$ を割りきる素数 $q\ge 3$ に対し以下の(a)から(c)を行う。

(a) $\text{mod }q$ での原始根 $g_q$ を見つける。
$1\le x\le q-2$ に対して $1-g_q{}^x=g_q{}^{f(x)}$ となるような $1\le f(x) \le q-2$ を計算する。
(b) $q-1$ を割りきる素数 $p$ に対し、 $k$ を $p^k \mid q-1$ かつ $p^{k+1} \nmid q-1$ なる整数とする。
Dirichlet指標 $\chi_{p,q}$ を、 $\chi_{p,q}(g_q{}^x) = \zeta_{p^k}{}^x$ で定義する。
(c) ・ $p \ge 3$ または $p=2$ かつ $k=2$ のとき、以下を計算する。
$\displaystyle J(p,q) = j(\chi_{p,q}, \chi_{p,q})= \sum_{1\le x \le q-2} \zeta_{p^k}{}^{x+f(x)}$

・ $p=2$ かつ $k\ge 3$ のとき、 $J(2,q)$ を上式で計算し、以下を計算する。
$\displaystyle J_3(q) = j(\chi_{2,q}, \chi_{2,q}) j(\chi_{2,q}, \chi_{2,q}{}^2)= J(2,q) \left( \sum_{1\le x \le q-2} \zeta_{2^k}{}^{2x+f(x)}\right)$

$\displaystyle J_2(q) = j(\chi_{2,q}{}^{2^{k-3}}, \chi_{2,q}{}^{3\cdot 2^{k-3}})^2 = \left( \sum_{1\le x \le q-2} \zeta_{8}{}^{3x+f(x)}\right)^2$

素数判定

素数判定したい数を $N$ ( $N\le B$ )とする。

Step1. $(t\cdot e(t), N)>1$ であれば、 $N$ は合成数である

Step2. $p\mid t$ に対して、
　　・ $p\ge 3$ かつ $N^{p-1}\not\equiv 1\quad \text{mod }p^2$ であれば、 $l_p\gets 1$
　　・それ以外であれば、 $l_p \gets 0$

Step3. $p^k \parallel (q-1) \mid t$ となる全ての素数のペア $(p,q)$ に対し
　　・ $p\ge 3$ のとき、Step 4aへ
　　・ $p=2$ かつ $k\ge 3$ のとき、Step 4bへ
　　・ $p=2$ かつ $k=2$ のとき、Step 4cへ
　　・ $p=2$ かつ $k=1$ のとき、Step 5へ

Step 4a. $E$ を $p^k$ 未満で $p$ と互いに素な自然数の集合とする。
　　・ $\Theta \gets \sum_{x\in E} x\sigma_x^{-1}$
　　・ $r\gets N \text{ mod }p^k$
　　・ $\alpha \gets \sum_{x\in E} \lfloor \frac{rx}{p^k} \rfloor \sigma_x^{-1}$
　　・ $s_1 \gets J(p,q)^\Theta \text{ mod } N$
　　・ $s_2 \gets s_1{}^{\lfloor N/p^k\rfloor} \text{ mod } N$
　　・ $S(p,q) \gets s_2 J(p,q)^\alpha \text{ mod } N$

　　このとき、 $S(p,q)\equiv \eta \text{ mod } N$ となるような $1$ の $p^k$ 乗根 $\eta$ が存在しないとき、 $N$ は合成数である。

　　もし $\eta$ が存在し、原始冪根であるとき、 $l_p\gets 1$ とする。

Step 4b. $E$ を $2^k$ 未満で $\text{mod }8$ で $1$ または $3$ に合同な自然数の集合とする。
　　・ $\Theta \gets \sum_{x\in E} x\sigma_x^{-1}$
　　・ $r\gets N \text{ mod }2^k$
　　・ $\alpha \gets \sum_{x\in E} \lfloor \frac{rx}{2^k} \rfloor \sigma_x^{-1}$
　　・ $s_1 \gets J_3(q)^\Theta \text{ mod } N$
　　・ $s_2 \gets s_1{}^{\lfloor N/2^k\rfloor} \text{ mod } N$
　　・ $S(2,q) \gets s_2 J_3(q)^\alpha J_2(q)^{\delta_N} \text{ mod } N$
　　　　　ここで $\delta_N$ は $N$ が $1$ か $3$ に合同であるときに $0$ 、それ以外は $1$ とする。

　　このとき、 $S(2,q)\equiv \eta \text{ mod } N$ となるような $1$ の $2^k$ 乗根 $\eta$ が存在しないとき、 $N$ は合成数である。

　　もし $\eta$ が存在し、原始冪根であり、かつ、 $q^{(N-1)/2}\equiv -1 \text{ mod }N$ のとき、 $l_2\gets 1$ とする。

Step 4c.
　　・ $s_1 \gets J(2,q)^2\cdot q \text{ mod } N$
　　・ $s_2 \gets s_1{}^{\lfloor N/4\rfloor} \text{ mod } N$
　　・ $N\equiv 1 \quad (\text{mod } 4)$ のとき、 $S(2,q) \gets s_2$
　　　 $N\equiv 3 \quad (\text{mod } 4)$ のとき、 $S(2,q)\gets s_2 J(2,q)^2$

　　このとき、 $S(2,q)\equiv \eta \text{ mod } N$ となるような $1$ の $4$ 乗根 $\eta$ が存在しないとき、 $N$ は合成数である。

　　もし $\eta$ が存在し、原始冪根であり、かつ、 $q^{(N-1)/2}\equiv -1 \text{ mod }N$ のとき、 $l_2\gets 1$ とする。

Step 4d.
　　・ $S(2,q)\gets (-q)^{(N-1)/2} \quad\text{mod }N$

　　このとき、 $S(2,q)\not\equiv \pm 1 \text{ mod } N$ であれば、 $N$ は合成数である。

　　もし $S(2,q)\equiv -1 \text{ mod } N$ かつ $N\equiv 1 \text{ mod } 4$ のとき、 $l_2\gets 1$ とする。

Step 5. $l_p=0$ なる $p\mid t$ に対して以下を行う。
　　・ $q\nmid e(t), p\mid(q-1)$ かつ $(q, N)=1$ となる $q$ をランダムに選ぶ。
　　・Step 4a-4dを $(p,q)$ に対して行う。
　　・何度か繰り返しても $0$ となる $l_p$ があれば「判定不能」を返す。（現実的にはこれはまず起こらない）

Step 6.
　　・ $i=1, \dots , t-1$ に対して、 $r_i\gets N^i\quad \text{mod } e(t)$ を計算する。
　　・もしある $i$ で $r_i$ が $N$ を割りきれば合成数である。そうでなければ素数と判定される。

以上がAPR-CL素数判定アルゴリズムです。
かなり場合分けが煩雑ですね。

上記アルゴリズムだけでは実装には悩む箇所があるので、実装上は[Coh-Len2]を参照するといいです。
$\sigma_x^{-1}$ を作用させる箇所や、1のべき根であることの判定法などが具体的に記載されています。

Python3による実装

[Cohen]とはできるだけ記号を合わせているので、比較しながら読めばわかるはず。
上のアルゴリズムで事前計算とされている部分は、事前計算にせずにその場で計算しています。
原始根なども保存せずに毎回計算したりしているので、少し工夫すればもう少しは早くなるかも。

手元の環境での実行時間は、100桁だと2秒、2^521-1（157桁）が18秒、2^1279-1（386桁）が5分55秒といったところで、まずまずの速度でしょうか。

GitHub - wacchoz/APR_CL: Adleman–Pomerance–Rumely-Cohen-Lenstra primality test (APR-CL)

# -*- coding: utf-8 -*-

import copy
import time
from math import gcd  # version >= 3.5



# primality test by trial division
def isprime_slow(n):
    if n<2:
        return False
    elif n==2 or n==3:
        return True
    elif n%2==0:
        return False
    else:
        i = 3
        while i*i <= n:
            if n%i == 0:
                return False
            i+=2
    return True        


# v_q(t): how many time is t divided by q
def v(q, t):
    ans = 0
    while(t % q == 0):
        ans +=1
        t//= q
    return ans


def prime_factorize(n):
    ret = []
    p=2
    while p*p <= n:
        if n%p==0:
            num = 0
            while n%p==0:
                num+=1
                n//= p
            ret.append((p,num))
        p+= 1

    if n!=1:
        ret.append((n,1))

    return ret


# calculate e(t)
def e(t):
    s = 1
    q_list = []
    for q in range(2, t+2):
        if t % (q-1) == 0 and isprime_slow(q):
            s *= q ** (1+v(q,t))
            q_list.append(q)
    return 2*s, q_list

# Jacobi sum
class JacobiSum(object):
    def __init__(self, p, k, q):
        self.p = p
        self.k = k
        self.q = q
        self.m = (p-1)*p**(k-1)
        self.pk = p**k
        self.coef = [0]*self.m

    # 1
    def one(self):
        self.coef[0] = 1
        for i in range(1,self.m):
            self.coef[i] = 0
        return self


    # product of JacobiSum
    # jac : JacobiSum
    def mul(self, jac):
        m = self.m
        pk = self.pk
        j_ret=JacobiSum(self.p, self.k, self.q)
        for i in range(m):
            for j in range(m):
                if (i+j)% pk < m:
                    j_ret.coef[(i+j)% pk] += self.coef[i] * jac.coef[j]
                else:
                    r = (i+j) % pk - self.p ** (self.k-1)                    
                    while r>=0:
                        j_ret.coef[r] -= self.coef[i] * jac.coef[j]
                        r-= self.p ** (self.k-1)

        return j_ret


    def __mul__(self, right):
        if type(right) is int:
            # product with integer
            j_ret=JacobiSum(self.p, self.k, self.q)
            for i in range(self.m):
                j_ret.coef[i] = self.coef[i] * right
            return j_ret
        else:
            # product with JacobiSum
            return self.mul(right)
    

    # power of JacobiSum（x-th power mod n）
    def modpow(self, x, n):
        j_ret=JacobiSum(self.p, self.k, self.q)
        j_ret.coef[0]=1
        j_a = copy.deepcopy(self)
        while x>0:
            if x%2==1:
                j_ret = (j_ret * j_a).mod(n)
            j_a = j_a*j_a
            j_a.mod(n)
            x //= 2
        return j_ret
    

    # applying "mod n" to coefficient of self
    def mod(self, n):
        for i in range(self.m):
            self.coef[i] %= n
        return self
    

    # operate sigma_x
    # verification for sigma_inv
    def sigma(self, x):
        m = self.m
        pk = self.pk
        j_ret=JacobiSum(self.p, self.k, self.q)
        for i in range(m):
            if (i*x) % pk < m:
                j_ret.coef[(i*x) % pk] += self.coef[i]
            else:
                r = (i*x) % pk - self.p ** (self.k-1)                    
                while r>=0:
                    j_ret.coef[r] -= self.coef[i]
                    r-= self.p ** (self.k-1)
        return j_ret
    
                
    # operate sigma_x^(-1)
    def sigma_inv(self, x):
        m = self.m
        pk = self.pk
        j_ret=JacobiSum(self.p, self.k, self.q)
        for i in range(pk):
            if i<m:
                if (i*x)%pk < m:
                    j_ret.coef[i] += self.coef[(i*x)%pk]
            else:
                r = i - self.p ** (self.k-1)
                while r>=0:
                    if (i*x)%pk < m:
                        j_ret.coef[r] -= self.coef[(i*x)%pk]
                    r-= self.p ** (self.k-1)

        return j_ret
    

    # Is self p^k-th root of unity (mod N)
    # if so, return h where self is zeta^h
    def is_root_of_unity(self, N):
        m = self.m
        p = self.p
        k = self.k

        # case of zeta^h (h<m)
        one = 0
        for i in range(m):
            if self.coef[i]==1:
                one += 1
                h = i
            elif self.coef[i] == 0:
                continue
            elif (self.coef[i] - (-1)) %N != 0:
                return False, None
        if one == 1:
            return True, h

        # case of zeta^h (h>=m)
        for i in range(m):
            if self.coef[i]!=0:
                break
        r = i % (p**(k-1))
        for i in range(m):
            if i % (p**(k-1)) == r:
                if (self.coef[i] - (-1))%N != 0:
                    return False, None
            else:
                if self.coef[i] !=0:
                    return False, None

        return True, (p-1)*p**(k-1)+ r
            

# find primitive root
def smallest_primitive_root(q):
    for r in range(2, q):
        s = set({})
        m = 1
        for i in range(1, q):
            m = (m*r) % q
            s.add(m)
        if len(s) == q-1:
            return r
    return None   # error


# calculate f_q(x)
def calc_f(q):
    g = smallest_primitive_root(q)
    m = {}
    for x in range(1,q-1):
        m[pow(g,x,q)] = x
    f = {}
    for x in range(1,q-1):
        f[x] = m[ (1-pow(g,x,q))%q ]

    return f


# sum zeta^(a*x+b*f(x))
def calc_J_ab(p, k, q, a, b):
    j_ret = JacobiSum(p,k,q)
    f = calc_f(q)
    for x in range(1,q-1):
        pk = p**k
        if (a*x+b*f[x]) % pk < j_ret.m:
            j_ret.coef[(a*x+b*f[x]) % pk] += 1
        else:
            r = (a*x+b*f[x]) % pk - p**(k-1)
            while r>=0:
                j_ret.coef[r] -= 1
                r-= p**(k-1)
    return j_ret


# calculate J(p,q)（p>=3 or p,q=2,2）
def calc_J(p, k, q):
    return calc_J_ab(p, k, q, 1, 1)

            
# calculate J_3(q)（p=2 and k>=3）
def calc_J3(p, k, q):
    j2q = calc_J(p, k, q)
    j21 = calc_J_ab(p, k, q, 2, 1)
    j_ret = j2q * j21
    return j_ret


# calculate J_2(q)（p=2 and k>=3）
def calc_J2(p, k, q):
    j31 = calc_J_ab(2, 3, q, 3, 1)
    j_conv = JacobiSum(p, k, q)
    for i in range(j31.m):
        j_conv.coef[i*(p**k)//8] = j31.coef[i]
    j_ret = j_conv * j_conv
    return j_ret


# in case of p>=3
def APRtest_step4a(p, k, q, N):

    print("Step 4a. (p^k, q = {0}^{1}, {2})".format(p,k,q))
    
    J = calc_J(p, k, q)
    # initialize s1=1
    s1 = JacobiSum(p,k,q).one()
    # J^Theta
    for x in range(p**k):
        if x % p == 0:
            continue
        t = J.sigma_inv(x)
        t = t.modpow(x, N)
        s1 = s1 * t
        s1.mod(N)

    # r = N mod p^k
    r = N % (p**k)

    # s2 = s1 ^ (N/p^k)
    s2 = s1.modpow(N//(p**k), N)

    # J^alpha
    J_alpha = JacobiSum(p,k,q).one()
    for x in range(p**k):
        if x % p == 0:
            continue
        t = J.sigma_inv(x)
        t = t.modpow((r*x)//(p**k), N)
        J_alpha = J_alpha * t
        J_alpha.mod(N)

    # S = s2 * J_alpha
    S = (s2 * J_alpha).mod(N)

    # Is S root of unity
    exist, h = S.is_root_of_unity(N)

    if not exist:
        # composite!
        return False, None
    else:
        # possible prime
        if h%p!=0:
            l_p = 1
        else:
            l_p = 0
        return True, l_p


# in case of p=2 and k>=3
def APRtest_step4b(p, k, q, N):

    print("Step 4b. (p^k, q = {0}^{1}, {2})".format(p,k,q))

    J = calc_J3(p, k, q)
    # initialize s1=1
    s1 = JacobiSum(p,k,q).one()
    # J3^Theta
    for x in range(p**k):
        if x % 8 not in [1,3]:
            continue
        t = J.sigma_inv(x)
        t = t.modpow(x, N)
        s1 = s1 * t
        s1.mod(N)

    # r = N mod p^k
    r = N % (p**k)

    # s2 = s1 ^ (N/p^k)
    s2 = s1.modpow(N//(p**k), N)

    # J3^alpha
    J_alpha = JacobiSum(p,k,q).one()
    for x in range(p**k):
        if x % 8 not in [1,3]:
            continue
        t = J.sigma_inv(x)
        t = t.modpow((r*x)//(p**k), N)
        J_alpha = J_alpha * t
        J_alpha.mod(N)

    # S = s2 * J_alpha * J2^delta
    if N%8 in [1,3]:
        S = (s2 * J_alpha ).mod(N)
    else:
        J2_delta = calc_J2(p,k,q)
        S = (s2 * J_alpha * J2_delta).mod(N)

    # Is S root of unity
    exist, h = S.is_root_of_unity(N)

    if not exist:
        # composite 
        return False, None
    else:
        # possible prime
        if h%p!=0 and (pow(q,(N-1)//2,N) + 1)%N==0:
            l_p = 1
        else:
            l_p = 0
        return True, l_p


# in case of p=2 and k=2
def APRtest_step4c(p, k, q, N):

    print("Step 4c. (p^k, q = {0}^{1}, {2})".format(p,k,q))

    J2q = calc_J(p, k, q)

    # s1 = J(2,q)^2 * q (mod N)
    s1 = (J2q * J2q * q).mod(N)

    # s2 = s1 ^ (N/4)
    s2 = s1.modpow(N//4, N)

    if N%4 == 1:
        S = s2
    elif N%4 == 3:
        S = (s2 * J2q * J2q).mod(N)
    else:
        print("Error")

    # Is S root of unity
    exist, h = S.is_root_of_unity(N)

    if not exist:
        # composite
        return False, None
    else:
        # possible prime
        if h%p!=0 and (pow(q,(N-1)//2,N) + 1)%N==0:
            l_p = 1
        else:
            l_p = 0
        return True, l_p


# in case of p=2 and k=1
def APRtest_step4d(p, k, q, N):

    print("Step 4d. (p^k, q = {0}^{1}, {2})".format(p,k,q))

    S2q = pow(-q, (N-1)//2, N)
    if (S2q-1)%N != 0 and (S2q+1)%N != 0:
        # composite
        return False, None
    else:
        # possible prime
        if (S2q + 1)%N == 0 and (N-1)%4==0:
            l_p=1
        else:
            l_p=0
        return True, l_p


# Step 4
def APRtest_step4(p, k, q, N):

    if p>=3:
        result, l_p = APRtest_step4a(p, k, q, N)
    elif p==2 and k>=3:
        result, l_p = APRtest_step4b(p, k, q, N)
    elif p==2 and k==2:
        result, l_p = APRtest_step4c(p, k, q, N)
    elif p==2 and k==1:
        result, l_p = APRtest_step4d(p, k, q, N)
    else:
        print("error")

    if not result:
        print("Composite")

    return result, l_p


def APRtest(N):
    t_list = [
        2,
        12,
        60,
        180,
        840,
        1260,
        1680,
        2520,
        5040,
        15120,
        55440,
        110880,
        720720,
        1441440,
        4324320,
        24504480,
        73513440
        ]

    print("N=", N)

    if N<=3:
        print("input should be greater than 3")
        return False
 
    # Select t
    for t in t_list:
        et, q_list = e(t)
        if N < et*et:
            break
    else:
        print("t not found")
        return False

    print("t=", t)
    print("e(t)=", et, q_list)

    # Step 1
    print("=== Step 1 ===")
    g = gcd(t*et, N)
    if g > 1:
        print("Composite")
        return False

    # Step 2
    print("=== Step 2 ===")
    l = {}
    fac_t = prime_factorize(t)
    for p, k in fac_t:
        if p>=3 and pow(N, p-1, p*p)!=1:
            l[p] = 1
        else:
            l[p] = 0
    print("l_p=", l)

    # Step 3 & Step 4
    print("=== Step 3&4 ===")
    for q in q_list:
        if q == 2:
            continue
        fac = prime_factorize(q-1)
        for p,k in fac:

            # Step 4
            result, l_p = APRtest_step4(p, k, q, N)

            if not result:
                # composite
                print("Composite")
                return False
            elif l_p==1:
                l[p] = 1

    # Step 5          
    print("=== Step 5 ===")
    print("l_p=", l)
    for p, value in l.items():
        if value==0:
            # try other pair of (p,q)
            print("Try other (p,q). p={}".format(p))
            count = 0
            i = 1
            found = False
            # try maximum 30 times
            while count < 30:
                q = p*i+1
                if N%q != 0 and isprime_slow(q) and (q not in q_list):
                    count += 1

                    k = v(p, q-1)
                    # Step 4
                    result, l_p = APRtest_step4(p, k, q, N)

                    if not result:
                        # composite
                        print("Composite")
                        return False
                    elif l_p == 1:
                        found = True
                        break
                i += 1
            if not found:
                print("error in Step 5")
                return False

    # Step 6
    print("=== Step 6 ===")
    r = 1
    for t in range(t-1):
        r = (r*N) % et
        if r!=1 and r!= N and N % r == 0:
            print("Composite", r)
            return False
    # prime!!
    print("Prime!")
    return True


if __name__ == '__main__':


    start_time = time.time()

    APRtest(2**521-1)   # 157 digit, 18 sec
#    APRtest(2**1279-1)  # 386 digit, 355 sec

    end_time = time.time()
    print(end_time - start_time, "sec")