DTAM論文を読んでみた
どうせ暇だしDTAM論文を読んでみます。
結構むずかしいです・・・
画像処理は専門ではなくて趣味で読んでるだけなので、適当なことを書いてるかもしれないがそのつもりで。
Richard A. Newcombe, Steven J. Lovegrove and Andrew J. Davison.
DTAM: Dense Tracking and Mapping in Real-Time, ICCV 2011
https://www.robots.ox.ac.uk/~vgg/rg/papers/newcombe_davison__2011__dtam.pdf
著者によるデモ動画はこちら。
www.youtube.com
画面上のすべてのピクセルについて深度を計算する、しかもリアルタイムに、というのが凄いです。

フレームrでの画像のピクセルの輝度は、フレーム
では、
となります。
ここではカメラの内部パラメータ行列、
はカメラ座標
からカメラ座標
への変換行列、
は
を
に射影する関数。また
は、射影後の点を、深度の逆数
としたときに、カメラ空間に戻す関数です。
同じ点は違う角度から見ても同じ輝度であると仮定します。
photometric errorを以下で定義します。
すると以下の式を最小化するようなdを計算する問題になります。
(右辺は隣接する数フレーム分の平均をとっています。)
しかしながら、これをそのまま計算しても、ノイズっぽくなってしまい残念な感じになります。
この計算自体は各ピクセル毎に独立に最小化すればいいわけですが、独立に行うことから滑らかさが一切ないことになります。
結果が滑らかになるように以下のようにregularisation term(第1項)を付け加えます。
を最小化する問題として定式化します。
ここで]は深度の逆数であり、求めたい関数です。
重み項は輝度の勾配から定義され、
ここで||・||はHuberノルムで、
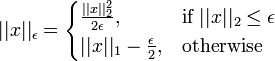
のように、と
の組み合わせです。
は深度を滑らかにするためであり、
は深度が不連続に変化することを許すそうです。
の効果により、輝度の勾配が大きいところでは、深度が不連続になることを許しています。
の第1項は凸関数で性質が良いのですが、第2項は凸関数ではなく、このままでは扱いづらい。
そこで以下の関数の最小化問題を解くことにします。
と
は両方とも未知なので、一見すると問題が複雑になっただけに見えます。
まずはとすると
となるのに注意。
そしてを固定すると、
となりますが、この問題は-ROF denoising問題の類似であり、効率的な解法が知られています。
またを固定すると、
となり、これは各ピクセルごとに最小化することができます。
つまり、
(1)初期値:
(2)を固定し、
を最小化する。
(3)を固定し、
を最小化する。
(4)を小さくする
を繰り返し収束させていけばよさげです。
ここでLegendre-Fenchel変換のお勉強を少し。
このあたりは以下の論文を読むとよいかもです。
Ankur Handa, Richard A. Newcombe, Adrien Angeli, Andrew J. Davison, Applications of Legendre-Fenchel transformation to computer vision problems
一般的な問題として、
という問題を考えます。
Legendre-Fenchel変換の定義から、
となります。
最初の最小化問題は、Dual Formとして
と書けます。
は凸なので、
が凸であれば、鞍点を求めるシンプルな問題になります。(多分)
さて元の問題に戻って、Legendre-Fenchelを適用してみます。
その前に元の問題をベクトルの形で少し書き換えます。
こんな感じで行列を1列に並べます。
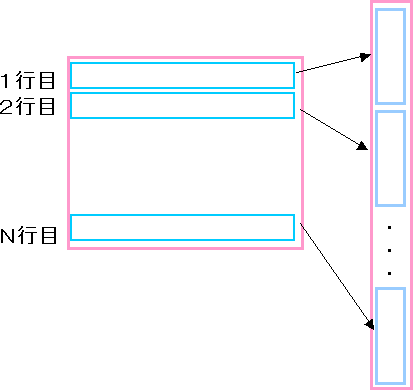
のベクトルバージョンとして
、
のベクトルバージョンを
、
もベクトルバージョンを
と表記することにします。
ベクトル表記すると
となります。
(とあるんだけど、ならないと思う。最初の積分の式で、を中に入れて、
にしないとならない気がする。こうしても次頁のアルゴリズムとも整合性がとれないような… 結局のところ
ではなかろうか)
Legendre-Fenchel変換により
となります。
ここでは、乗算でgradを計算できるような成分をもった行列です。
(Mingqiang Zhu, Fast Numerical Algorithms for Total Variation Based Image Restorationを参照)
またです。

これにより
と書けます。
(1)
,
を計算する。
(2)を固定して、
に関してminを探しに山を下り、
に関してmaxを探しに山を上る。
(3)次にを固定して、
に関してminを探す。これはピクセル毎に行える。
(4)を減らす
を繰り返せばよいようです。
論文中の(1)のの式は符号が1箇所間違っているかと思います。
やはり以下の論文の7.4あたりを読むといいかも。 Ankur Handa, Richard A. Newcombe, Adrien Angeli, Andrew J. Davison, Applications of Legendre-Fenchel transformation to computer vision problems
(2)のステップはGPU等で並列計算できます。多分(3)も出来ます。
PS. 論文の数式は何箇所か間違ってそうです。自分で式変形していったほうがいいかも。