某女の子が歌ったり踊ったりするゲームの何か(2)
どうせ暇なので、過去のプログラムの在庫整理の続き。
シェーダで描画を改善してみる。
かなり見栄えが良くなりました。
シェーダの中身は某プログラムのパクリです。ごめんなさい。
いずれどうにかするかも。
ちゃんとフラグでシェーダを切り替えてないので、正しく描画されないモデルもあるけど、そのうち・・・
これは結構大変でいつになるやら・・・
「マルチバイト文字セットを使用する」でビルドして下さい。
ライブラリはCgを追加で使用しています。
(2013/5/5差し替え)
(2018/11 GitHubに移動)
こんな感じです。

スキニングの話(3)
次はDual Quaternionを使ったスキニング手法。
Ladislav Kavan et al.,2008, Geometric skinning with approximate dual quaternion blending, ACM Trans. Graph. 27, 4, 105.
Quaternionは回転しか表せず、平行移動は表せないのがとっても不満です。
Dual Quaternionはその不満を解消するツールです。
Dual Quaternionは
のように定義されます。
ここでは"dual unit"と呼ばれ、
という特殊な規則に従う数です。
、
は普通のQuaternionであり、前者はnon-dual part、後者はdual partと呼ぶことにします。
Quaternionとの積は可換です。
さて、回転を表すdual quaternionはnon-dual partのを0とし、
とするだけ。つまり今までのquaternionと同じだ。
では今までと変わったのは何かというと、平行移動を表せることだ。
平行移動を表すには
のようnon-dual partを1とし、dual partに平行移動成分を持たせたものとなる。
2で割るのは回転のquaternionのときと似ている。
平行移動と回転移動を合成するには普通に乗算すればよい。
さて、実際に頂点にdual quaternionを作用させるには、まず頂点座標を
のように変換し、
とすればよい。
回転と平行移動を合成するというよりは、平行移動しながら回転するという螺旋的なイメージの方が合っている。
実際、
というdual quaternionを考えてみる。と
は両方ともdual quaternionである。
これは螺旋軸に沿った回転と平行移動を表す。
は回転角を表し、
は螺旋軸に沿った平行移動量を表す。
または螺旋軸の向きの単位ベクトルを表す。
だけわかりにくいのだが、回転中心を
としたとき、
となる。
さてこれをスキニングにどう使うのか。
まず回転を表すquaternionと平行移動を合成して、dual quaternionを作る。
これをボーンウェイトに従って線形補間する。
このdual quaternionを使って頂点を変換すればよい。
この変換について、論文中に高速化の方法が書かれているため、実装する際には参照するとよい。
スキニングの話(2)
Linear Blend Skinningでしばしばおかしな変形を目にすることになる。
一例を図に示す。
(Ladislav Kavan et al.,Geometric Skinning with Approximate Dual Quaternion Blendingより引用)

頂点は
と
から50%ずつ影響されているとする。
ボーンアニメーションにより、は動かず、
が180°回転したとする。
このときの影響で
に変換され、
の影響で
に変換されるため、50%ずつの重みにより平均した結果、
は
に一致してしまい、完全にメッシュがつぶれてしまう。
"candy-wrapper"と呼ばれる現象である。
これは重みつき平均を計算する際、単純に線形に平均してしまったことに起因する。
は回転せず、
は180°回転しているため、本来であれば
は90°回転となってほしいところである。
(+90°なのか-90°なのかという曖昧さは残っているが…)
この例を見ていると、回転をQuaternionでの球面線形補間とするという発想が生まれてくる。
この手法は以下の論文に論じられている。
KAVAN, L., AND ZARA, J. 2005. Spherical blend skinning: A real-time deformation of articulated models. In 2005 ACM SIGGRAPH Symposium on Interactive 3D Graphics and Games, ACM Press, 9–16
回転を補間するのであるが、回転の中心点がどこであるかというのが論文中では詳しく書かれている。
上例のように隣接するボーン2つから影響される場合は単純である。回転中心は誰がどう見てもである。
さてを回転部
と移動部
に分解しよう。
とし、さらにをクォータニオン
に変換しよう。
と
の回転部のクォータニオンを適切に補間したものを
とすると、
]
とすればよい。
これがSpherical Blend Skinningの手法である。
クォータニオンの補間に球面線形補間を使うのが自然であるが、補間計算は頂点毎に行う必要があるため、球面線形補間を行うのは処理が重過ぎる。(arccosが1回にsinが2回)
単純に線形補間を行い正規化してもそれほど誤差がないそうである。
さて上例では隣接したボーンから影響される頂点について考えていた。
このため、を回転中心に選ぶというシンプルな計算であった。
実際には3本以上のボーンから影響される頂点もあるし、隣接しないボーン2本から影響される場合もある。
このような場合にはどのように回転中心を選べばよいであろうか?
まず上例の場合では、回転中心は
という関係が成り立っていたことに注目する。
一般に個のボーンに影響されている場合、回転中心
は
により定義することができる。
これはが3以上では優決定系であり、一般的には解が存在しないため、最小二乗法により解くことになる。
回転中心が決まれば、以下の式で変換後の頂点が計算できる。
しかしながらこの手法が3本以上のボーンなどの一般の場合に使われるかどうか微妙である。
何しろ回転中心の計算はボーンの組み合わせ毎に行わなければならず、面倒すぎるのだ。
スキニングの話(1)
どうせ暇だしスキニングについて書いてみる。
スキニングとは3Dアニメーションで使われる手法で、ポリゴン内部にボーンを仕込んでおき、ボーンを動かすことでポリゴンを変形させる手法である。
骨格構造はジョイント(関節)の集合である。
そしてジョイントとは単なる点ではなく、ジョイントを原点とする座標系を意味すると考えたほうがよい。それぞれのジョイントに座標系があるわけだ。
各ポリゴンはそれぞれのジョイント(で定義される座標系)からどれだけ影響されているかという重みを与えられている。
ではボーンは何かというと、親子関係のあるジョイント間を線で結んだだけのものである。人間にとってわかりやすくするための便宜上のものといえる。

まず初期姿勢(rest pose)で考えよう。
両手を左右に伸ばして立っているあの姿勢である。
でジョイント
を原点とする座標系からモデル空間へ変換行列を表すことにする。
たとえばを原点とする座標系の原点は、モデル空間での座標は、
で表すことができる。
同様に、でジョイント
を原点とする座標系からジョイント
を原点とする座標系に変換する行列としよう。
ジョイントは親から順にと繋がっているとすると、ジョイント
を原点とする座標系をモデル空間に変換する行列は、
と書ける。
またモデル空間からジョイントを原点とする座標系への変換は、この行列の逆行列であり、
と書ける。
さてアニメーションとは、
行列は初期姿勢のときの行列として用いたため、アニメーションにより変化したときの行列は
で表すことにしよう。
時刻でのジョイント
からモデル空間への変換行列を
とする。
同様に
である。
ある初期姿勢でのメッシュ上の点がジョイント
にのみ影響されているとしよう。
このとき点の、ジョイント
を原点とする座標系での座標は、
となる。
この点を時刻でのモデル空間での座標に変換すると、
となる。これがボーンアニメーションの基本である。
しばしばとまとめて書かれることもある。
ここまでは点がジョイント
のみに影響されるとしてきたが、複数のジョイントに影響される場合も同様であり、ジョイント
にそれぞれ重み
で影響されるとした場合、
とする方法がLinear Blend Skinningである。 この方法は広く用いられ、そしてしばしば問題を引き起こす。(つづく)
Quaternionと回転の話
どうせ暇だしQuaternionについてまとめてみる。
Quaternion(クォータニオン)は3次元グラフィクス分野でよく出てくるツールである。
もともとはHamiltonによって考案された概念で、複素数の自然な拡張となっている。
単位複素数がGauss平面上での回転を表すことは高校数学で学んだ通り。
原点周りにθだけ回転させるには、複素数に
を乗算すればよいのであった。
さて3次元上での回転は、複素数を拡張したQuaternionで表すことができる。
以下のように定義される。
ここで、i, j, kは
と定義される。
この定義からすぐに従うが、
となる。つまり乗法は非可換である。
3次元上の回転は回転の順序により結果が変わるというのは広く知られるところだが、Quaternionの非可換性はこれと対応するものだ。
Quaternionは複素数の拡張であると言ったが、類似する性質を見ていこう。
単位Quaternionを
と書こう。
このとき複素数と同様に
が成り立つのである。
なお、一般に単位Quaternionは
と書ける。
さて、Quaternionを用いてどのように点を回転させるのか見ていこう。
これが回転軸の回りに回転角
での回転をあらわすQuaternionである。
複素数の場合とは違い、単純に頂点座標に乗算するわけではない。
頂点座標を
のようにQuaternionに変換しておく。
このとき、
のように左右から乗算することで、p'の各成分が、頂点pを回転した座標となる。
回転の合成は回転行列の場合と同様で、Quaternionを単純に乗算すればよい。
Quaternionが重宝される理由の1つは回転の補間が容易にできることである。
3次元グラフィクスでは、回転と回転
の間を最短距離で等速になるよう補間したいと思うことがしばしばある。
Quaternionを使うことにより、球面線形補間とよばれる式でこのような補間が可能となる。
以下のが
と
の球面線形補間である。
ここでである。
なおのときは
を
で置き換える必要があるとのこと。
(も
も同じ回転を表す)
さて少し違う話題。
複素数に戻ろう。
について対数をとると
となる。(簡便のため、対数の主値のみを記載)
これを見ると、対数をとると回転角を取り出せることがわかる。
実は同様のアナロジーがQuaternionにも成り立つ。
について、
が成り立つ。
つまり対数をとると、回転角と回転軸が取り出されるのである。
ネイピアが対数を発明したモチベーションは、乗算や除算を加減算で行うことで煩雑な計算を楽にすることであった。
Quaternionについて対数を用いて乗算を加算にすることができるだろうか。
そもそも対数で乗算を加算にできるのは、
が成り立つためであった。
Quaternionの場合には乗算の非可換性のために、この式が成り立たない。
Baker-Campbell-Hausdorffの公式とよばれる
が成り立つ。
つまりQuaternionの場合には、対数をとり加算してから指数関数をとっても、乗算した場合と結果が一致しないのである。
しかしながら近似的には成り立ちそれなりに便利なため、たまに使われるようだ。
某女の子が歌ったり踊ったりするゲームの何か
Standing on the shoulders of giants
2年以上前に書いてたプログラムの在庫整理。
とりあえずはモデルの表示まで。
かつてOpenGLバージョンとDirectXバージョンを作ったけど、今回はOpenGLバージョンを整理。
整理というほどは整理できてないんだけど。。。
ライブラリはGLUT、GLUI、libsquish、DirectX9を使用しています。
libsquishはVS2010以上の*.slnファイルが用意されていないので自分で作って下さい。
DirectX9は今回のうpに限って言えばD3DXVECTOR3などの型を利用してるだけなので、ほぼ不要です。
GLUIは初めて使ってみたけど、回転操作が簡単に実装できるのが良いです。
正しい使い方をしているのか自信が無いけどあしからず。
テクスチャはDXT形式なので、DirectXならヘッダを付ければそのまま読めるのですが、OpenGLなのでlibsquishでRGBAに展開しています。
*.exeファイルのショートカットを作って、ショートカットの上にファイルをドラッグ&ドロップすると便利です。
(2013/4/6 差替え/前にうpしたものがコンパイル通ってませんでした)
(2018/11 GitHubに移動)
こんな感じです。

ワイヤフレーム表示

DTAM論文を読んでみた
どうせ暇だしDTAM論文を読んでみます。
結構むずかしいです・・・
画像処理は専門ではなくて趣味で読んでるだけなので、適当なことを書いてるかもしれないがそのつもりで。
Richard A. Newcombe, Steven J. Lovegrove and Andrew J. Davison.
DTAM: Dense Tracking and Mapping in Real-Time, ICCV 2011
https://www.robots.ox.ac.uk/~vgg/rg/papers/newcombe_davison__2011__dtam.pdf
著者によるデモ動画はこちら。
www.youtube.com
画面上のすべてのピクセルについて深度を計算する、しかもリアルタイムに、というのが凄いです。

フレームrでの画像のピクセルの輝度は、フレーム
では、
となります。
ここではカメラの内部パラメータ行列、
はカメラ座標
からカメラ座標
への変換行列、
は
を
に射影する関数。また
は、射影後の点を、深度の逆数
としたときに、カメラ空間に戻す関数です。
同じ点は違う角度から見ても同じ輝度であると仮定します。
photometric errorを以下で定義します。
すると以下の式を最小化するようなdを計算する問題になります。
(右辺は隣接する数フレーム分の平均をとっています。)
しかしながら、これをそのまま計算しても、ノイズっぽくなってしまい残念な感じになります。
この計算自体は各ピクセル毎に独立に最小化すればいいわけですが、独立に行うことから滑らかさが一切ないことになります。
結果が滑らかになるように以下のようにregularisation term(第1項)を付け加えます。
を最小化する問題として定式化します。
ここで]は深度の逆数であり、求めたい関数です。
重み項は輝度の勾配から定義され、
ここで||・||はHuberノルムで、
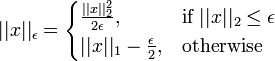
のように、と
の組み合わせです。
は深度を滑らかにするためであり、
は深度が不連続に変化することを許すそうです。
の効果により、輝度の勾配が大きいところでは、深度が不連続になることを許しています。
の第1項は凸関数で性質が良いのですが、第2項は凸関数ではなく、このままでは扱いづらい。
そこで以下の関数の最小化問題を解くことにします。
と
は両方とも未知なので、一見すると問題が複雑になっただけに見えます。
まずはとすると
となるのに注意。
そしてを固定すると、
となりますが、この問題は-ROF denoising問題の類似であり、効率的な解法が知られています。
またを固定すると、
となり、これは各ピクセルごとに最小化することができます。
つまり、
(1)初期値:
(2)を固定し、
を最小化する。
(3)を固定し、
を最小化する。
(4)を小さくする
を繰り返し収束させていけばよさげです。
ここでLegendre-Fenchel変換のお勉強を少し。
このあたりは以下の論文を読むとよいかもです。
Ankur Handa, Richard A. Newcombe, Adrien Angeli, Andrew J. Davison, Applications of Legendre-Fenchel transformation to computer vision problems
一般的な問題として、
という問題を考えます。
Legendre-Fenchel変換の定義から、
となります。
最初の最小化問題は、Dual Formとして
と書けます。
は凸なので、
が凸であれば、鞍点を求めるシンプルな問題になります。(多分)
さて元の問題に戻って、Legendre-Fenchelを適用してみます。
その前に元の問題をベクトルの形で少し書き換えます。
こんな感じで行列を1列に並べます。
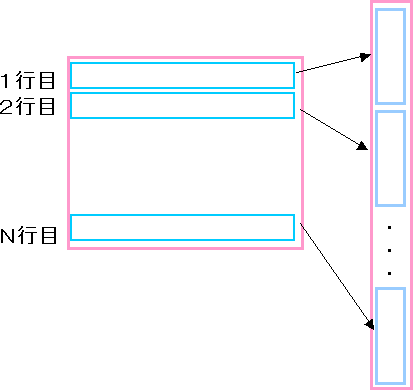
のベクトルバージョンとして
、
のベクトルバージョンを
、
もベクトルバージョンを
と表記することにします。
ベクトル表記すると
となります。
(とあるんだけど、ならないと思う。最初の積分の式で、を中に入れて、
にしないとならない気がする。こうしても次頁のアルゴリズムとも整合性がとれないような… 結局のところ
ではなかろうか)
Legendre-Fenchel変換により
となります。
ここでは、乗算でgradを計算できるような成分をもった行列です。
(Mingqiang Zhu, Fast Numerical Algorithms for Total Variation Based Image Restorationを参照)
またです。

これにより
と書けます。
(1)
,
を計算する。
(2)を固定して、
に関してminを探しに山を下り、
に関してmaxを探しに山を上る。
(3)次にを固定して、
に関してminを探す。これはピクセル毎に行える。
(4)を減らす
を繰り返せばよいようです。
論文中の(1)のの式は符号が1箇所間違っているかと思います。
やはり以下の論文の7.4あたりを読むといいかも。 Ankur Handa, Richard A. Newcombe, Adrien Angeli, Andrew J. Davison, Applications of Legendre-Fenchel transformation to computer vision problems
(2)のステップはGPU等で並列計算できます。多分(3)も出来ます。
PS. 論文の数式は何箇所か間違ってそうです。自分で式変形していったほうがいいかも。